Um die Welleneigenschaften von immer größeren und größeren Molekülen nachzuweisen bedienen sich Forscher oft gefinkelter experimenteller Methoden. Unter anderem machen sie sich dabei ein optisches Phänomen zu Nutze das Talbot Teppich heißt. Was sich hinter diesem Namen verbirgt und wie das aussieht, darum wirds in diesem Artikel gehen.
Was bisher geschah
Teil 1 – Die Geschichte von Materiewellen bis 1927
Teil 2 – Materiewellen und Talbot Teppiche
Im letzten Beitrag ging es darum wie Physiker Schritt für Schritt auf die Idee kamen auch Materieteilchen Welleneigenschaften zuzuschreiben und wie sie sich von den Ideen ihrer Vorgänger inspirieren ließen. Wir sind in weiterer Folge auf die Schrödingergleichung gestoßen und eine nützliche Analogie zur Wellenoptik, bis wir schließlich nach einem kurzen Exkurs zur Beugung von Röntgenstrahlung and Kristallgittern beim Nachweis der Wellennatur von Elektronen gelandet sind.
Hier machen wir nun einen kurzen Ausflug in die Wellenoptik. Dafür sehen wir uns zunächst ein ganz grundlegendes Phänomen an das wir uns im Anschluss dann zunutze machen werden – die Interferenz.
Interferenz
Eine geläufige Situation in der man es mit Interferenz zu tun hat ist, wenn man zwei Steine nebeneinander ins Wasser plumpsen lässt. Zuerst werden sich Wellen grob kreisförmig um die Steine ausbreiten bis sie schließlich aufeinandertreffen. An diesen Stellen verstärken sich die Wellen oder schwächen sich gegenseitig ab – je nachdem ob Wellentäler, Wellenberge oder irgendetwas dazwischen aufeinandertreffen. Genau das bezeichnet man als Interferenz, und das sehen wir uns gleich etwas detaillierter an!
Treffen also zwei Wellen verschiedener Wellenlänge oder Phase aufeinander, so kann dies zu einem recht komplexen und faszinierenden, fast hypnothischen, Ergebnis führen:

Es gibt hierbei aber zwei interessante Spezialfälle! Einer davon liegt dann vor, wenn die beiden ursprünglichen Wellen genau in Phase sind, also sozusagen immer genau ein Wellenberg mit einem Wellenberg überlappt, und ein Wellental mit einem Wellental. In solch einer Situation verstärken sich die beiden Wellen, es kommt zu konstruktiver Interferenz:

Es ist aber auch möglich, dass sich beide Wellen vollständig auslöschen. Dazu muss eine von den beiden um eine halbe Wellenlänge phasenverschoben sein. Dies bedeutet, dass nun ein Wellenberg jeweils auf ein Wellental trifft – und umgekehrt. Es geht sich in Summe genau so aus, dass die resultierende Welle überall, flapsig formuliert, Auslenkung $0$ hat.

Wellen können also auf diese Art miteinander wechselwirken. Sehen wir uns doch ein konkretes Beispiel an.
Interferenz von Laserlicht
Wir benötigen drei Zutaten – einen Laser, ein feines Gitter und eine Art Detektor. Im Prinzip kann der Detektor ein Blatt Papier sein, aber um etwas quantitativer zu messen bieten sich CCD Kameras an.
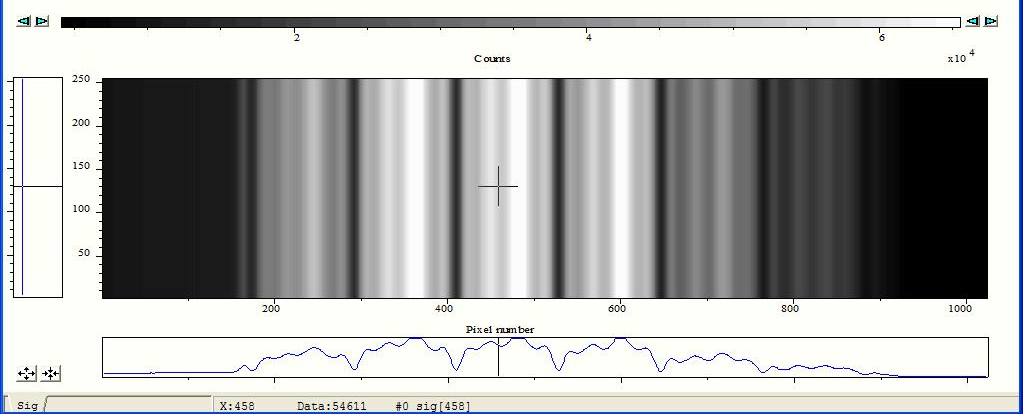
Ein Laser wird (von links kommend) durch ein feinmaschiges Gitter geschickt und am Ort des Blatt Papiers ist schließlich ein Interferenzmuster zu sehen. Der Aufbau ist allerdings nicht ganz ideal, das Muster wird durch andere Effekte überlagert. Ein mit einer CCD Kamera aufgezeichner Ausschnitt zeigt das was man erwarten würde schon deutlicher:
Das Bild zeigt jenes Interferenzmuster das sich dann ergibt, wenn ein Helium Neon Laser (Wellenlänge $632.8\,\text{nm}$) durch ein feinmaschiges Gitter geschickt wird. Während noch andere Effekte zum Tragen kommen ist deutlich zu sehen, dass sich helle Bereiche (etwa 100 Pixel breit) mit schmaleren dunkleren abwechseln. Am Ort des Detektors findet also abwechselnd konstruktive und destruktive Interferenz statt.
Die Gitterkonstante, nebenbei bemerkt, muss, damit sich diese Welleneigenschaft des Lichts zeigen lässt, in etwa in der Größenordnung der Laserwellenlänge liegen – oder anders gesagt – durchlässige und undurchlässige Stellen dürfen nicht viel größer sein als etwa der Durchmesser eines menschlichen Haars.
Ein feinmaschiges Gitter verglichen mit einem menschlichen Haar. Das Haar hat in etwa denselben Durchmesser wie die lichtdurchlässigen und lichtundurchlässigen Spalten des Gitters (etwa $40\,\mu\text{m}$)
Talbot Teppiche
Und das bringt uns nun zum Talbot Teppich. Das zuvor gezeigte Muster bildet sich dann, wenn der Detektor sich weit weg genug weg vom Gitter befindet, man spricht in diesem Fall von Fernfeldbeugung. In ausreichender Distanz kann die Krümmung der Wellenfronten vernachlässigt werden. Befindet man sich jedoch näher am Gitter, dort wo diese Vereinfachung nicht mehr zulässig ist, wird das Muster etwas komplexer. Zuerst entdeckte wurde dies bereits 1836 von Henry Talbot.
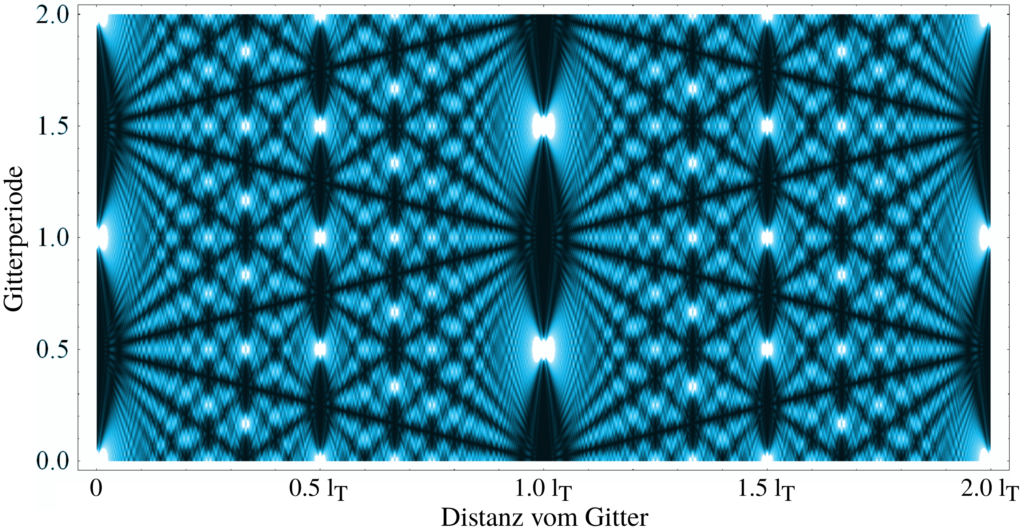
Ein Abbild des Gitters wiederholt sich verkleinert immer und immer wieder, und irgendwann ergibt sich wieder das Gitter in seiner Originalgröße. Von links nach rechts gehend gesehen stellt man zuerst bei $1.0\,l_T$ fest, dass das Bild des Gitters wieder so groß ist wie das Original. Allerdings ist es um eine halbe Gitterperiode entlang der y-Achse verschoben! Geht man noch weiter nach rechts findet man schließlich eine exakte Reproduktion – und zwar bei $2.0\,l_T$. Hierbei ist $l_T$ die Talbot Länge, welche von der Gitterkonstante und der Wellenlänge des Lichts abhängt:
\[ l_T = \frac{d_G^2}{\lambda} \]
Für einen roten Helium-Neon Laser mit $\lambda=632.8\,\text{nm}$ und einem Gitter mit Gitterkonstante $40\,\mu\text{m}$ ergäbe sich eine Talbot Länge von $2.5\,\text{mm}$. Ein virtuelles Experiment zum Talbot Effekt kann man übrigens auf quantumnano.at durchführen!
So weit so gut! Wie sich jetzt Quantenphysiker den optischen Talbot Effekt zu Nutze machen, darum wirds beim nächsten Mal gehen.
Literatur
H. F. Talbot. Facts relating to optical science. no. iii. London and Edinburgh philosophical magazine and journal of science, 9:001–004, 1836.