Die Pyramiden Ägyptens sind ein Stoff, um den sich vielerlei Mythen und Legenden ranken. Man kann sich ihnen aber auch auf wissenschaftliche Art und Weise nähern um ihren noch verbleibenden Geheimnissen Schritt für Schritt auf die Spur zu kommen und sie zu lösen. Zum Beispiel ist man auf der Suche nach noch nicht entdeckten und versteckten Kammern und Passagen. Gar nicht so leicht, wenn man nicht destruktiv vorgehen will. Immerhin hat man es im Prinzip mit einem unbeweglichen Haufen Kalkstein zu tun. Wie also ins Innere sehen ohne etwas zu zerstören? Und vor allem – wo kommt da die Relativitätstheorie ins Spiel?

Hohlräume in Pyramiden

Geschehnisse in der Atmosphäre

Anstatt auf die Pyramiden richten wir unseren Blick zunächst auf die Atmosphäre etwa $15\,\text{km}$ darüber. Dort oben trifft kosmische Strahlung auf Atomkerne in Luftmolekülen, und die hohe Energie der Kollisionen führt zur Bildung neuer Teilchen. Dabei bilden sich Protonen, Neutronen, Kaonen, Photonen, Elektronen, Positronen, und so weiter. Aber für uns ist gerade die Bildung von geladenen Pionen – also $\pi^+$ oder $\pi^-$ geschrieben, am interessantesten. Am häufigsten zerfallen diese nämlich wenige Meter später mittels der schwachen Wechselwirkung auf folgende Weise:

\[\pi^+ \rightarrow \mu^+ + \nu_\mu \]

\[\pi^- + \rightarrow \mu^- + \bar{\nu}_\mu \]

Also in Myonen $\mu^-$ und Antimyonen $\mu^+$, aber auch einen alten Bekannten – das Myon Neutrino $\nu_\mu$ und Myon Antineutrino $\bar{\nu}_\mu$. Mehr zu Neutrinos gibts aber in einem anderem Artikel zu lesen.

Myonen und Relativitätstheorie

Das Myon jedenfalls saust nach seiner Entstehung mit fast Lichtgeschwindigkeit weiter Richtung Erdoberfläche, und die hohe Geschwindigkeit hat eine spannende Konsequenz. Die Halbwertszeit eines Myons beträgt nämlich nicht ganz $\tau_{1/2} = 2.2\,\mu\text{s}$, also 2.2 Mikrosekunden. Nun kann man sich überlegen, wie weit es denn zu seiner Lebzeit mit seiner Geschwindigkeit überhaupt kommen würde:

\[ s = c\,\tau_{1/2} \approx 660\,\text{m} \]

mit $c$ als Lichtgeschwindigkeit und $s$ als Distanz

[expand title=“Die Sache mit der Halbwertszeit…“]

Man muss natürlich vorsichtig sein von Halbwertszeit zu sprechen, wenn man es mit einem einzelnen Teilchen zu tun hat. In so einem Fall versteht man darunter allerdings, dass das Partikel mit $50\,\text{%}$ Wahrscheinlichkeit innerhalb der Halbwertszeit zerfällt. Gemeinhin wird es mit zunehmender Zeit immer unwahrscheinlicher, dass ein Teilchen noch nicht zerfallen ist. Im Folgenden beschränken wir uns der Einfachheit halber auf Myonen, welche genau nach $2.2\,\mu\text{s}$ zerfallen.

[/expand]

Das Myon würde also, selbst wenn es mit Lichtgeschwindigkeit unterwegs wäre, $660\,\text{m}$ nach seiner Entstehung bereits wieder in etwas Anderes zerfallen – also immer noch in fast $15\,\text{km}$ Höhe! Natürlich kann es nie Lichtgeschwindigkeit erreichen, tatsächlich ist es ein bisschen langsamer. Somit zerfällt das Myon sogar noch näher an seinem Entstehungsort. Eigentlich würde man daher erwarten, diese an der Erdoberfläche nicht mehr messen zu können – und dennoch tut man genau das. Tatsächlich können Myonen auch noch Kilometer darunter detektiert werden. Was geht hier also vor?

Das Geheimnis lässt sich lüften, wenn man die spezielle Relativitätstheorie heranzieht. Der Fehler steckt in unserer Berechnung zu $s$, denn bei Geschwindigkeiten die ein signifikanter Bruchteil der Lichtgeschwindigkeit sind, machen sich die Effekte der Relativiätstheorie bemerkbar. Aber wie dramatisch ist’s nun wirklich?

Auf ihrer Reise Richtung Erdoberfläche, und auch danach, verlieren Myonen Energie durch verschiedene Prozesse wie zum Beispiel die Ionisation anderer Luftmoleküle oder durch die Abgabe von Bremsstrahlung. Auf Meeresniveau haben sie im Mittel jedoch noch immer eine Energie von etwa $4\cdot 10^9\,\text{eV}$. Die Einheit eV ist in der Teilchenphysik üblich, ausgeschrieben bedeutet dies Elektronenvolt. Sie gibt die Energie eines Teilchens in Vielfachen der Energie an, die ein Elektron hat, wenn es in einer Spannung von $1\,\text{V}$ beschleunigt wird.

Das Ganze lässt sich jedenfalls über die  relativistische Energie in eine Geschwindigkeit umrechnen – und führt auf etwa $0.99965 c$. Das ist tatsächlich ziemlich flott. Ein Funksignal zum Mond braucht etwa $1.2435\,\text{s}$ – ein Myon mit obiger Geschwindigkeit, sofern es denn nicht vorher zerfiele, träfe nur eine halbe tausendstel Sekunden später ein. Zum Vergleich: Die Astronauten der Apollo 11 Mission benötigten für (fast) diesselbe Strecke beinahe 52 Stunden.

[expand title=“Geschwindigkeit des Myons“]

Die relativistische Gesamtenergie ist gegeben durch

\[ E = \sqrt{c^2 p^2 + (m_0 c^2)^2}. \]

Hierbei ist $m_0=105.7\,\text{MeV}$ die Ruhemasse des Myons und $p$ der relativistische Impuls. Dieser wiederum lässt sich anschreiben als

\[ p = \frac{m_0 v}{\sqrt{1-\frac{v^2}{c^2}}}, \]

mit $v$ als Geschwindigkeit des Myons. Etwas Umformen führt letztlich auf

\[ v = \frac{\sqrt{c^2 (E^2-c^4 m_0^2)}}{E} \]

Werden schließlich noch alle Größen in SI Einheiten umgerechnet, ergibt sich nach Einsetzen direkt die Geschwindigkeit $v$ in $\text{m/s}$.

[/expand]

Der Fehler in unserer Berechnung von $s$ lag nun darin, dass wir die relativistische Zeitdilatation nicht berücksichtigt haben. Wenn sich etwas relativ zu uns mit hoher Geschwindigkeit bewegt wird dieser Effekt allerdings merkbar. Während das Myon aus seiner Sicht nur $2.2\,\mu\text{s}$ lebt, sieht das aus unserer Perspektive anders aus. Durch Zeitdilatation überlebt es in unserem Bezugssystem fast $38$ mal so lange! So schafft das Myon anstatt der $660\,\text{m}$ etwa $25\,\text{km}$. Das ist mehr als genug, um am Erdboden noch detektierbar zu sein.

Natürlich kann man sich auch in die Lage des Myons versetzen, sich ansehen, was in seinem Bezugssystem passiert. Ein durchschnittliches Myon überlebt hier tatsächlich nicht länger als $2.2\,\mu\text{s}$. Allerdings verkürzt sich aus seiner Sicht die Distanz zum Erdboden. Diese beträgt anstatt der ursprünglichen $15\,\text{km}$ nun nur mehr knapp $400\,\text{m}$. Auch wenn es aus seiner Sicht bereits nach $660\,\text{m}$ wieder zerfällt, ist die sogenannte Längenkontraktion mehr als genug um den Erdboden nahe genug heranrücken zu lassen, um ihn noch erreichen zu können.

Myonen erreichen also den Erdboden und die Relativitätstheorie hilft uns zu verstehen, warum. Aber wie bringt uns das auf Hohlräume in Pyramiden?

Myonen Tomographie

Wie Eingangs erwähnt hätte man hier (so wie auch in anderen Fällen) gerne zerstörungsfreie Methoden um herauszufinden, was sich in den dicken Mauern einer Pyramide so befindet. Ein Durchbohren könnte Hieroglyphen, Malereien oder andere Kunstgegenstände auf der nicht einsehbaren Seite unwiderbringlich zerstören.

Das Prinzip der Myonen Tomographie ist grundsätzlich ähnlich zum dem von Röntgen. Mit Röntgenstrahlung kann, z.B. der menschliche Körper „durchleuchtet“ werden, mit Myonen auch eine Pyramide oder ein Vulkan. Dort wo mehr Strahlung/Teilchen durchtreten wird der Film/Detektor stärker belichtet, und umgekehrt. Durch kosmische Strahlung und die dadurch ausgelöste kontinuierliche Produktion von Myonen steht zusätzlich – quasi gratis – eine konstante Quelle dieser Teilchen zur Verfügung, die zu einem Großteil in etwa von oben kommen. Durch eine Fläche von einem Quadratzentimeter saust auf Meereshöhe pro Minute in etwa ein Myon.

Beim Durchqueren von Luft verlieren Myonen weniger Energie als in dichterer Materie (zum Beispiel Wasser oder Gestein). In Luft kann ein Myon also eine weitere Strecke zurücklegen bevor es zerfällt, als es dies in Gestein könnte. In der nächsten Abbildung ist das Prinzip bildlich dargestellt.

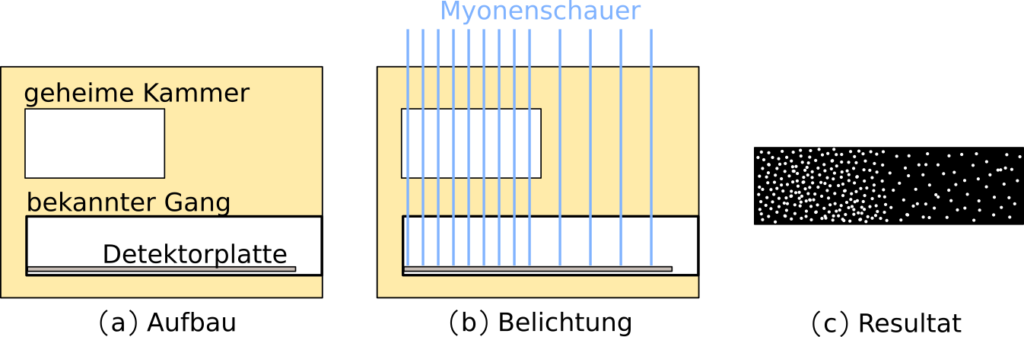
Teilbild (a) zeigt den groben Aufbau. Anstatt einer Pyramide sehen wir uns dies der Einfachheit halber anhand eines quaderförmigen Gebildes an. In diesen hinein geht ein bekannter Gang, und Experten vermuten eine geheime Kammer oberhalb dieses Ganges. Also schafft man Detektoren heran, im Bild als eine große Platte dargestellt, welche im Gang platziert werden.

Anschließend, zu sehen in Teilbild (b), belässt man diese dort für einige Zeit und lässt eine große Zahl an Myonen auf den Detektor treffen. In die folgende Überlegung beziehen wir auch wieder jene Myonen mit ein, die nicht genau zur Halbwertszeit zerfallen. Jene, welche nicht die geheime Kammer passieren und somit einen längeren Weg in Gestein zurücklegen, werden stärker verlangsamt als ihre Kollegen die zwischenzeitlich eine kurze Auszeit bekommen wenn sie durch die mit Luft gefüllte geheime Kammer fliegen. Manche von ihnen zerfallen nun einfach bevor sie den Detektor überhaupt erreichen können. Das gilt natürlich auch für ihre weniger verlangsamten Kollegen, aber von diesen betrifft es nur einen kleineren Anteil.

Nach Ablauf der Belichtungsphase zeigt Teilbild (c) schließlich das Ergebnis – im linken Bereich trafen deutlich mehr Myonen auf als im rechten, was auf einen über dem Gang liegenden Hohlraum schließen lässt.

In der Praxis

In der Praxis ist es natürlich etwas komplizierter, noch unbekannte Hohlräume in Pyramiden zu finden. Myonen kommen nicht perfekt von oben und die Pyramide ist – offensichtlich – nicht quaderförmig wie in unserem Beispiel. Dennoch sind diese Komplikationen in den Griff zu bekommen. Durch Simulationen zum Beispiel kann man einen guten Eindruck bekommen, was man ohne darüberliegenden Hohlraum an einem Detektor erwarten würde. Der Vergleich mit Messungen liefert dann einen Eindruck davon, wie wahrscheinlich ein Hohlraum als Erklärung für eine beobachtete Abweichung von der Simulation ohne Hohlräume ist.

Das folgende Bild zeigt nun den Aufbau der Cheops Pyramide, bzw. einen Schnitt durch diese entlang der Nord-Süd Achse.

So sieht es dann aus, wenn die Detektoren angebracht werden. Im betrachteten Fall sind dies Emulsionsplatten (vermutlich aus einer Gelatine/Silber-Brom Kristall Mischung bestehend) welche in der Kammer der Königin platziert werden.

Diese Detektoren wurden auch an anderen Stellen verwendet – unter anderem im absteigenden Gang nahe des nördlichen Eingangs, noch bevor sich dieser teilt (in der vorvorigen Abbildung ganz rechts unten zu sehen) und in der unteren Kammer – wie der Name sagt in der vorvorigen Abbildung ganz unten.

Die vorläufigen und noch unpublizierten Ergebnisse für die Messungen im absteigend Gang legen nun nahe, dass sich darüber ein oder mehrere Hohlräume befinden. Möglicherweise sogar ein Gang, der etwas tiefer in die Pyramide führt. Solange noch nichts publiziert ist, sind die momentanen Schlussfolgerungen natürlich noch mit Vorsicht zu genießen.

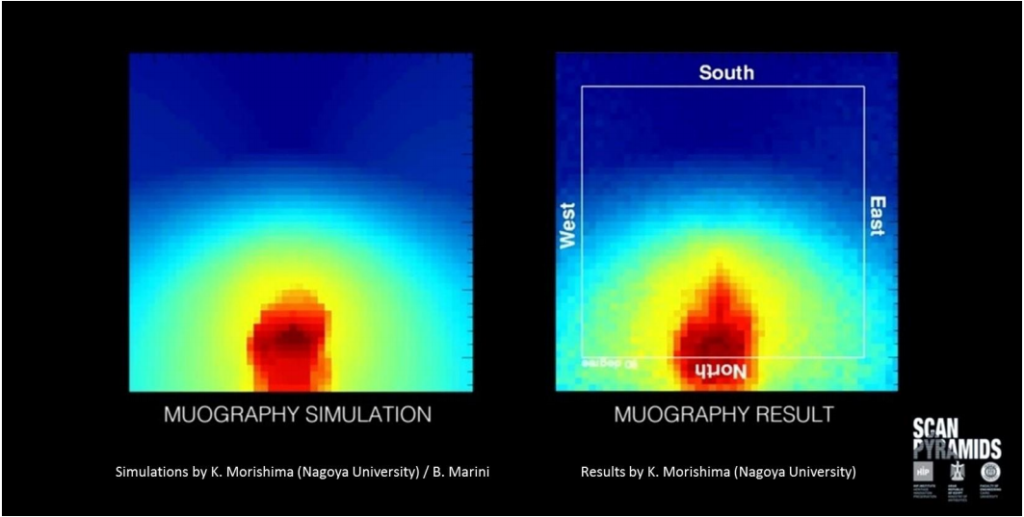
Die Forscher haben sich auch die Frage gestellt, wie wahrscheinlich so etwas durch statistische Schwankungen im Myonenfluss oder Rauschen im Messsignal entstehen kann. Die Wahrscheinlichkeit dafür scheint allerdings nur $1\cdot 10^{-6}\,\text{%}$ zu betragen (Scan Pyramids Press Release 10/2016).

Alles in allem scheint es also starke Indizien für weitere Hohlräume zu geben. Tatsächlich wurden auch noch andere Methoden angewandt, und in der Presseaussendung werden noch weitere Indizien für Hohlräume an anderen Stellen vorgestellt.

In jedem Fall stellt das Ganze für mich ein spannendes Beispiel dafür dar, wie verschiedenste Forschungsbereiche zusammenarbeiten, um Ergebnisse aus wieder andereren Bereichen anzuwenden um Antworten auf alte Rätsel zu finden. Archäologen, Teilchenphysiker, Techniker tun sich zusammen um Teilchen, deren Verhalten nur mittels Relativitätstheorie verstanden werden kann, zu verwenden, um Hohlräume in Pyramiden zu finden.

Literatur

Particle Data Group

Cosmic Rays and Muons

Gaisser, T. K., & Stanev, T. (2000). Cosmic rays. The European Physical Journal C-Particles and Fields, 15(1), 150-156.

Scan Pyramids Press Release, June 7th 2016, Cairo

Scan Pyramids Press Release, October 15th 2016, Cairo