Vor etwas mehr als einem Monat saß ich Abends in Linz auf den Stufen beim Ars Electronica Center, der Mond war voll und hell und blitzte immer mal wieder zwischen den Wolken hervor. Doch etwas links vom Mond war eine weitere, schwächere Lichtquelle zu sehen. Nachdem ich diese ein paar Minuten beobachtet hatte war ich mir sicher, dass diese nicht durch irgendeinen Scheinwerfer am Erdboden, oder durch an höher gelegenen Wolken durch ein Loch in der tieferen Wolkenschicht reflektiertes Mondlicht entstanden war. Da ich aber keine weiteren Möglichkeiten hatte das ganze genauer zu analysieren, machte ich einfach mit meinem Handy das eingangs zu sehende Foto. Inzwischen hatte ich etwas Zeit dieses auszuwerten und etwas herumzurechnen und siehe da – es könnte sich tatsächlich um einen sogenannten Nebenmond gehandelt haben. Wie man bei der Analyse des Bildes vorgehen kann und wie Nebenmonde entstehen – darum wird es hier gehen.
Wie entstehen Nebensonnen und Nebenmonde?
Nebenmonde entstehen auf die selbe Weise wie Nebensonnen – dem Phänomen und dem dahinterliegenden Mechanismus haben wir uns bereits ausführlich gewidmet, aber zusammenfassend lässt sichs so sagen:
In der Atmosphäre müssen, damit dieses Phänomen sichtbar wird, dünne sechseckige Eiskristalle vorkommen deren Grundfläche parallel zum Erdboden orientiert ist. Das von der Sonne oder eben dem Mond kommende Licht bricht sich in diesen dann auf charakteristische Weise und ist, wie in der folgenden Abbildung skizziert, von einem Beobachter unter einem bestimmten Winkel wahrnehmbar.
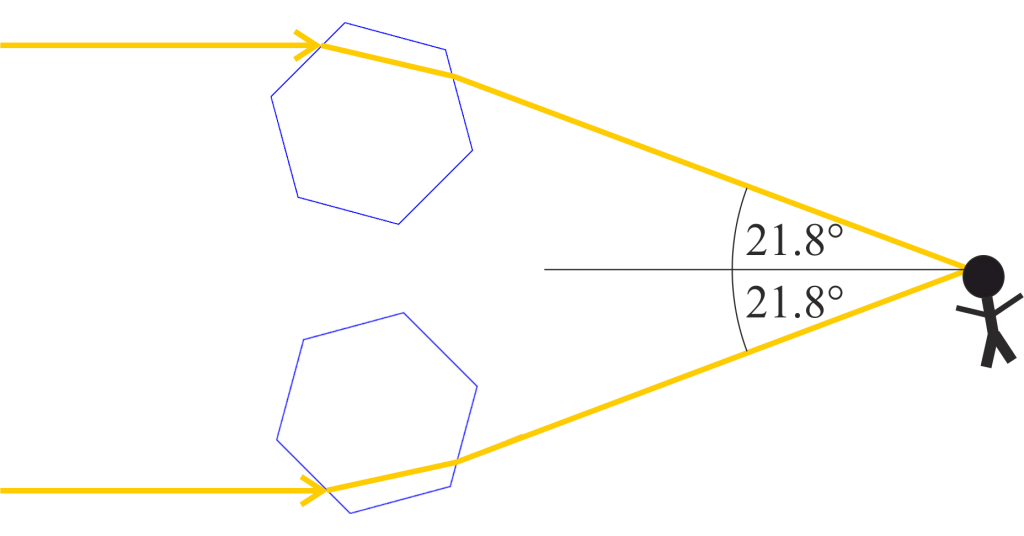
Insgesamt ergibt sich, für gelb-oranges Licht der Wellenlänge $589\;\text{nm}$, dass im Bereich zwischen $21^o$ und etwa $33^o$ ein Lichtfleck zu sehen ist welcher bei etwa $21.8^o$ am hellsten erscheint.
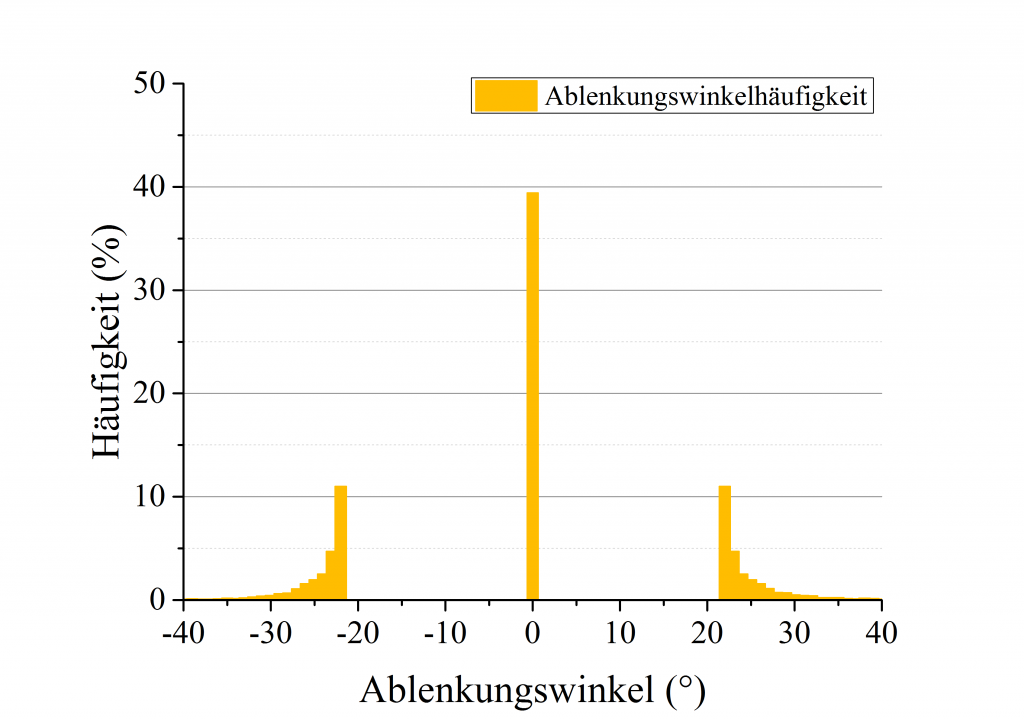
Ein Foto – was nun?
Ein Charakteristikum von Nebensonnen ist also der Winkel zwischen Sonne (bzw. Mond) und dem Lichtfleck. Wenn wir aus dem Foto diesen Winkel $\varphi$ rekonstruieren können, und $\varphi\approx 21.8^o$ dann würde uns das einen Hinweis liefern, ob das Lichtphänomen im Foto ein Nebenmond sein könnte.
Wie lässt sich nun aus einem Foto der Winkel eruieren?
Öffnungswinkel des Kameraobjektivs
Aufgenommen habe ich das Bild mit meinem OnePlus One Smartphone. Was genau passiert aber eigentlich wenn wir ein Foto mit einer Kamera machen? Unabhängig davon, ob dies eine Handykamera, Spiegelreflex oder Kompaktkamera ist.
Ein Ausschnitt der „realen Welt“ wird dabei durch das Linsensystem der Kamera auf den Film oder einen CCD Chip abgebildet. In zweiterem Fall ergibt sich damit, nachdem der Chip ausgelesen und die Daten verarbeitet wurden, ein Bild mit den Abmessungen von $x$ mal $y$ Pixeln.
Die Kamera bildet auch nicht einen beliebig großen Ausschnitt der Welt ab sondern nur einen begrenzten Teil davon welcher von zwei Winkeln beschrieben wird. Horizontal können wir alles innerhalb des Winkels $\Phi$ auf den Chip bannen, vertikal bis zu einem Winkel von $\Theta$.
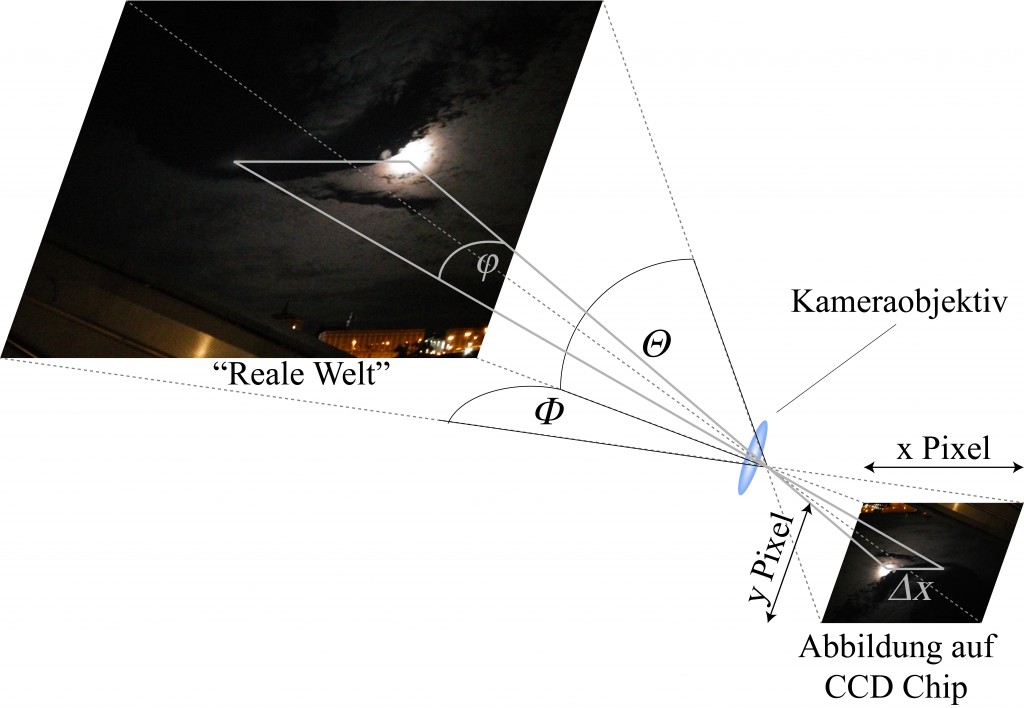
Die in der Skizze oben angedeuteten Winkel werden auch horizontaler Öffnungswinkel $\Phi$ bzw. vertikaler Öffnungswinkel $\Theta$ des Objektivs genannt.
[expand title=“Eigentlich…“]
Tatsächlich ist der Bereich den das Objektiv abbilden kann durch einen Kreis begrenzt und durch einen einzigen Winkel beschreibbar. Da aber der Chip auf den abgebildet wird eine rechteckige Form aufweißt, ist das Bild welches wir schließlich erhalten natürlich auch in dieser Form, und somit macht es Sinn für die Beschreibung einen horizontalen $\Phi$ und einen vertikalen Öffnungswinkel $\Theta$ heranzuziehen.
[/expand]
Hier ist auch bereits die Strategie zu erahnen die wir verfolgen um den Winkel $\varphi$ zwischen Mond und Lichtphänomen zu bestimmen – wir können, wenn wir $\Phi$ bestimmen, einen Umrechnunsgfaktor $u$ berechnen welcher uns sagt, wieviele Winkelgrad wievielen Bildpixeln entsprechen. Dieser ist gegeben durch
\[ u = \frac{\Phi}{x}\]
Wenn wir nun noch die Pixel zwischen Mond und Lichtphänomen $\Delta x$ zählen ergibt sich der Winkel zwischen den beiden aus
\[ \varphi = u \cdot \Delta x \]
Das alles folgt daraus, dass gilt
\[\frac{\varphi}{\Phi}=\frac{\Delta x}{x}\]
Es gibt also, da wir $\varphi$ berechnen wollen, nur eine Unbekannte! Wie bestimmen wir allerdings dieses $\Phi$?
Öffnungswinkel bestimmen
Im Prinzip gibt es eine sehr einfache Methode. Dazu habe ich das Smartphone auf einen Tisch gelegt und aus dieser Höhe ein am Boden liegendes Maßband fotografiert. Das Prinzip ist in der nächsten Abbildung für den vertikalen Öffnungswinkel gezeigt, funktioniert aber genauso für den horizontalen.
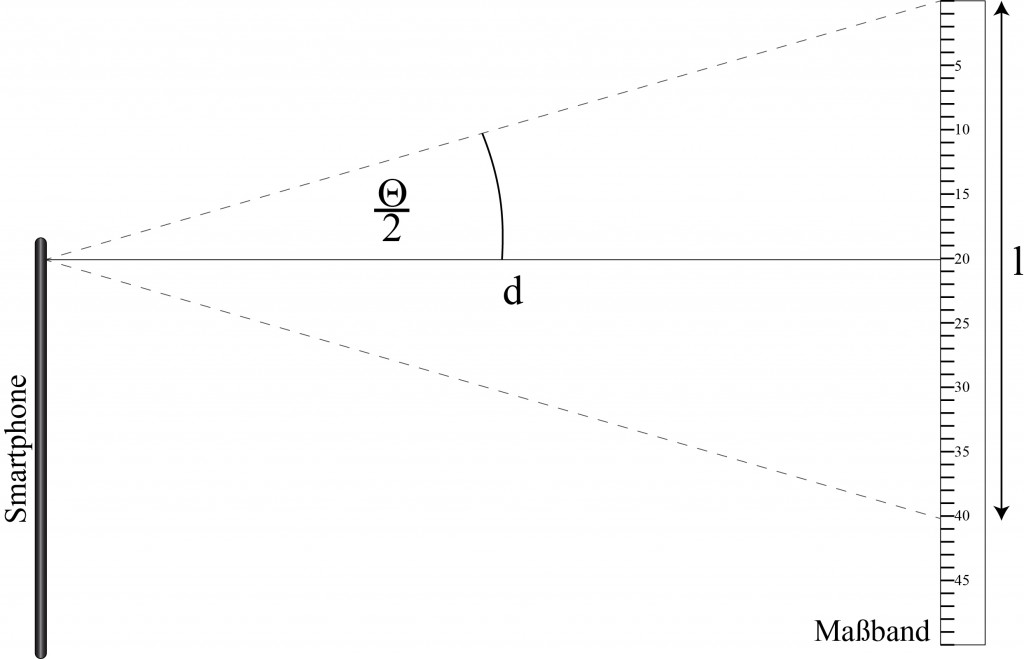
Wir fotografieren ein Maßband im Abstand $d$ zum Objektiv. Auf dem Bild stellen wir dann fest, dass wir insgesamt eine Länge von $l$ abfotografieren konnten. Der Öffnungswinkel des Objektives ist dann:
\[\Theta=2\arctan{\frac{l}{2d}}\]
Genauso können wir für den horizontalen Öffnungswinkel vorgehen (sofern wir das Maßband im Querformat abfotografieren). Um den Abstand $d$ leicht bestimmen zu können habe ich das Smartphone auf einen Tisch gelegt.

Es ist
\[l=(91.1\pm 0.5)\;\text{cm}\quad\text{und}\quad d=(75\pm 0.2)\;\text{cm}\]
und daher
\[\Phi=(62.6\pm 0.3)^o\]
Jetzt bleibt noch übrig die Pixel zwischen Mond und Lichtphänomen zu zählen:

Also haben wir nun auch
\[\Delta x=(1465\pm 50)\;\text{Pixel}\]
und die Breite des Bildes erfahren wir aus der Kamerasoftware oder den Dateieigenschaften
\[x=4160\;\text{Pixel}\]
Einsetzen in die zuvor hergeleiteten Gleichungen ergibt schließlich den gesuchten Winkel
\[\varphi=(22\pm 0.8)^o \]
Konklusion
Die fotografierte Lichterscheinung ist also etwa $22^o$ vom Mond entfernt und ist zumindest bis etwa $25^o$ noch sichtbar. Alles in allem ist dies ein starkes Indiz dafür, dass es sich tatsächlich um einen Nebenmond gehandelt hat. Intuitiv ist es vielleicht etwas schwerer vorstellbar, dass es auch im Sommer Eiskristalle in der Atmosphäre geben kann. Bedenkt man allerdings, dass die Lufttemperatur in der Troposphäre mit ca. $6^o/\text{km}$ fällt (siehe hier), so könnte es tatsächlich schon ab etwa $4\;\text{km}$ Höhe kalt genug gewesen sein. Besonders deutlich wird dies auf Flugreisen – die Temperatursensoren zeigen in $10\;\text{km}$ Flüghöhe Außentemperaturen von ca. $-60^o\text{C}$ an.
Auch, dass sich ein leichter Farbverlauf von rötlich bis blau (vom Mond weg) erahnen lässt spricht dafür, dss es sich um einen Nebenmond handelt.
Damit aber nicht genug. Eine Recherche brachte mich zum Beispiel auf diese sommerliche Nebenmondbeobachtung am 7.6.2009 von Alexander Pikhard und Natalie Ebner in Wien. Auf der verlinkten Seite gibt es auch eine wunderschöne Aufnahme des Phänomens zu sehen!
Alles in allem gibt es also plausible Gründe anzunehmen, dass hier tatsächlich ein sommerlicher Nebenmond zu sehen war.