Vor einiger Zeit habe ich ein bisschen was zu Nebensonnen geschrieben, einem optischen Phänomen das auftritt, wenn Eiskristalle  auf bestimmte Weise in der Atmosphäre orientiert vorkommen. Während eines Fluges vor ein paar Wochen habe ich wieder etwas gesehen – eine sogenannte Glorie. Was das ist und weshalb man beim Versuch sie zu erklären mit geometrischer Optik schlechte Karten hat, mit dem werden wir uns in diesem Artikel beschäftigen.

Glorien

Glorien entstehen durch die Wechselwirkung von Licht mit feinen Wassertröpfchen in Wolken oder Nebeln. Sie bestehen aus einem hellem Zentrum (das ist im Foto von mir leider nicht so gut zu sehen in dem unterhalb jedoch schon) und mehreren konzentrischen Ringen wobei jeder Ring innen bläulich und außen rötlich ist, mit einem regenbogenähnlichem Farbverlauf dazwischen. Je weiter außen der Ring desto transparenter wirkt er. Oben kann gerade noch der zweite Ring erahnt werden. Glorien schließen einen Winkel von 5° bis 20° ein. Zu beobachten sind sie immer der Sonne entgegengesetzt – im Bild unten ist dies deutlich sichtbar, im Zentrum des mehrfarbigen Ringes ist der Schatten des Ballonkorbes zu sehen.

Auch mitgefilmt habe ich etwas, im Video wandert die Glorie aufgrund der Drehung des Flugzeugs von links nach rechts durchs Bild.

Gleich vorweg: Wenn man recherchiert wie Glorien entstehen entdeckt man, dass dies noch nicht vollständig bzw. zufriedenstellend geklärt ist. Es ist nämlich noch nicht ganz klar was der Mechanismus ist, welcher diese Lichterscheinungen verursacht. Rein mit geometrischer Optik lässt sich dieses Phänomen nämlich nicht verstehen und die wellenoptische Erklärung hat den Nachteil eher unanschaulich zu sein. Natürlich muss ein Modell nicht anschaulich sein um erfolgreich die Natur beschreiben zu können, damit ist aber nicht gesagt, dass es nicht vielleicht doch intuitiver geht.

Versuchen wir dies zunächst dennoch mit geometrischer Optik nachzuvollziehen. Aber was wollen wir eigentlich beschreiben? Glorien können wie eingangs erwähnt von erhöhten Standpunkten aus immer der Sonne entgengesetzt beobachtet werden und weißen ein helles Zentrum mit weißem Licht auf um welches herum sich konzentrische, regenbogenfarbene Ringe zeigen. Forscht man etwas genauer nach stellt man auch fest, dass das Licht das von ihnen ausgeht polarisiert ist, also zumindest einmal innerhalb des Wassertropfens reflektiert wurde. Konzentrieren wir uns jedoch zunächst auf die erste Beobachtung – das Licht der Sonne wird im hellen Zentrum der Glorie um etwa $180^o$ zurückgeworfen, daher erscheint dieses heller.

Wie weit kommen wir mit geometrischer Optik?

Brechungsindex von Wasser

Für unsere Überlegungen müssen wir auf jeden Fall den Brechungsindex von Wasser kennen – denn eine Wolke besteht ja aus sehr vielen feinen Tröpfchen.

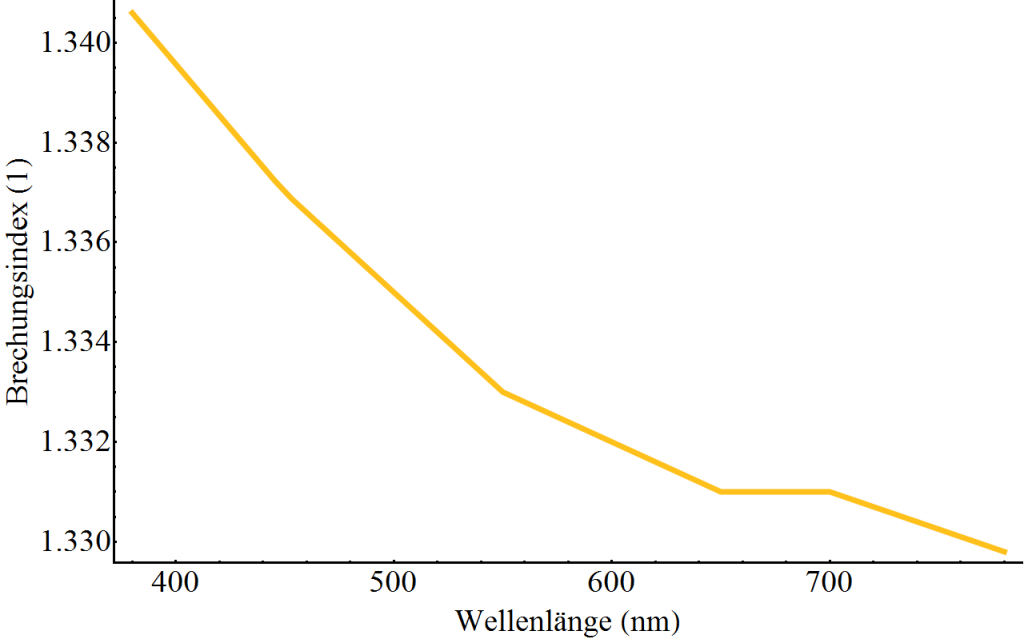
Wir sehen hier also bereits, dass rotes Licht (größere Wellenlängen) schwächer gebrochen wird als blaues Licht (kürzere Wellenlänge).

Einfallswinkel, Reflektivität und Fresnell Gleichungen

Als nächstes ist für uns interessant, wie gut ein Wassertropfen Lichtstrahlen fast direkt in Richtung der Sonne „zurückwerfen“ kann. Dazu bedienen wir uns wieder der Regeln der geometrischen Optik wie wir sie schon im Artikel über Nebensonnen kennengelernt haben. Den Wassertropfen stellen wir uns als Sphäre mit einem Radius von etwa $10\;\mu\text{ m}$ vor. Da die Sonne weit weg ist und der Tropfen sehr klein können wir die eintreffenden Lichtstrahlen als parallel annehmen. Einen Überblick verschafft die nächste Abbildung – diese gibt auch gleich darüber Aufschluss wie die Einfallswinkel im Fall einer Sphäre, bzw. bei Projektion in die Ebene einer Scheibe, bestimmt werden.

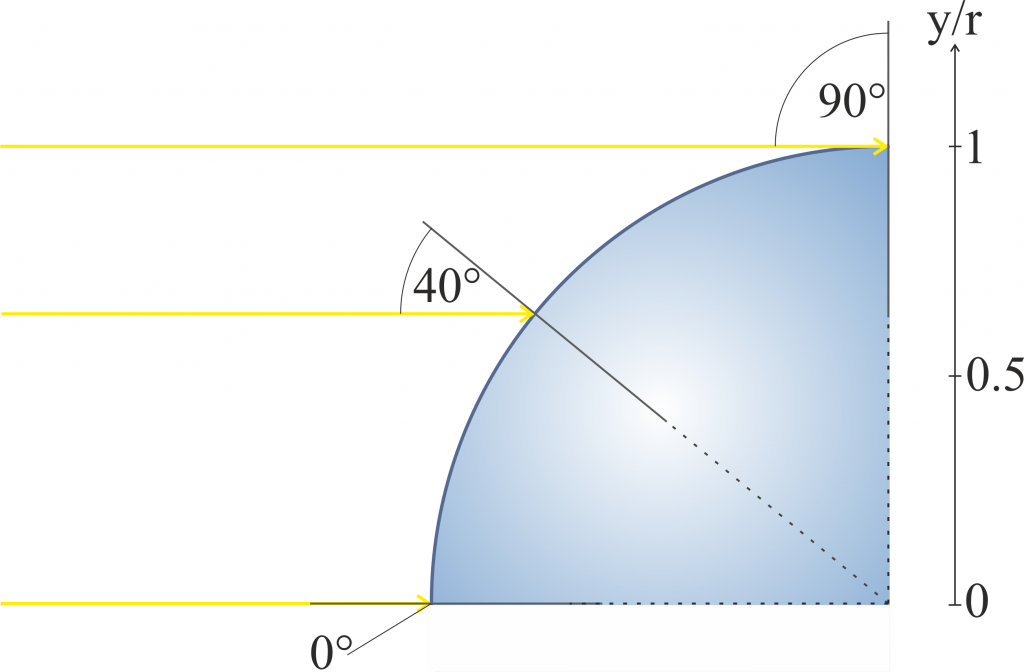
Wir beschränken uns zusätzlich noch auf Lichtstrahlen die in den Wassertropfen eintreten, dann einmal teilweise reflektiert werden, und wieder austreten. Mehrfachreflektionen im Inneren des Tropfens können wir deshalb vernachlässigen, weil der reflektierte Strahlteil mit jeder Reflektion stark abgeschwächt wird.

Von jenen Strahlen die in den Tropfen eintreten wird ein gewisser Bruchteil von deren Energie an der Grenzfläche reflektiert. Ein Teil des ursprünglichen Strahls tritt also in das Tröpfchen ein während ein gewisser Anteil zurückreflektiert wird (Ausfallswinkel = Einfallswinkel). Könnten diese Reflektierten Teilstrahlen denn einen nennenswerten Beitrag zur Glorie leisten? Nach Konsultation der Fresnell Gleichungen stellen wir fest: Nein, denn der Anteil der reflektiert wird macht nur ca. $1/50$tel der Energie des ursprünglichen Strahls aus. Zumindest solange der Einfallswinkel unter $40^o$ liegt – und in diesem Bereich müsste aber mehr zusammenkommen, damit damit der helle Bereich der Glorie erklärt werden könnte. Das ganze ist in der Abbildung unten veranschaulicht.

Zusätzlich wird abgesehen von dem Lichtstrahl mit Einfallswinkel $0^o$ kein anderer genau in sich selbst, und somit direkt zur Lichtquelle hin, zurückreflektiert. Auch dieser Umstand spricht dafür, dass wir diese Vernachlässigung machen können.

Werten wir also die Fresnellgleichungen aus und sehen uns an welcher Bruchteil eines Lichtstrahls, der unter einem bestimmten Winkel auf den Tropfen auftrifft, reflektiert wird:

\[ R_S = \left|\frac{n_1 \cos{\Theta_i} – n_2 \cos{\Theta_t}}{n_1 \cos{\Theta_i} + n_2 \cos{\Theta_t}}\right|^2 \]

\[ R_P = \left|\frac{n_1 \cos{\Theta_t} – n_2 \cos{\Theta_i}}{n_1 \cos{\Theta_t} + n_2 \cos{\Theta_i}}\right|^2 \]

dabei ist $R_S$ der Reflektionskoeffizient von Licht das senkrecht zur Einfallsebene polarisiert ist (in unserem Fall ist die Einfallsebene der Bildschirm), $R_P$ jener für parallel zu dieser Ebene polarisiertem Licht, $\Theta_i$ der Einfallswinkel und $\Theta_t$ der durch das Snellius’sche Gesetz gegebene Ausfallswinkel.

Da Sonnenlicht unpolarisiert ist können wir den Mittelwert aus beiden Koeffizienten bilden und erhalten

\[ R = \frac{R_S + R_P}{2} \]

Diese mittlere Reflektivität liegt zum Beispiel für blaues Licht bei Einfallswinkeln unterhalb von $40^o$ bei etwa $2\;\%$, erst darüber wird ein signifikanter Teil des Lichtstrahls zurückreflektiert:

Also können wir auch die vor dem Eintritt in den Tropfen bereits reflektierten Strahlteile vernachlässigen.

Der Weg von Licht durch den Tropfen

Sehen wir uns an, was laut geometrischer Optik mit einem weißen Lichtstrahl passiert der auf den Tropfen auftrifft:

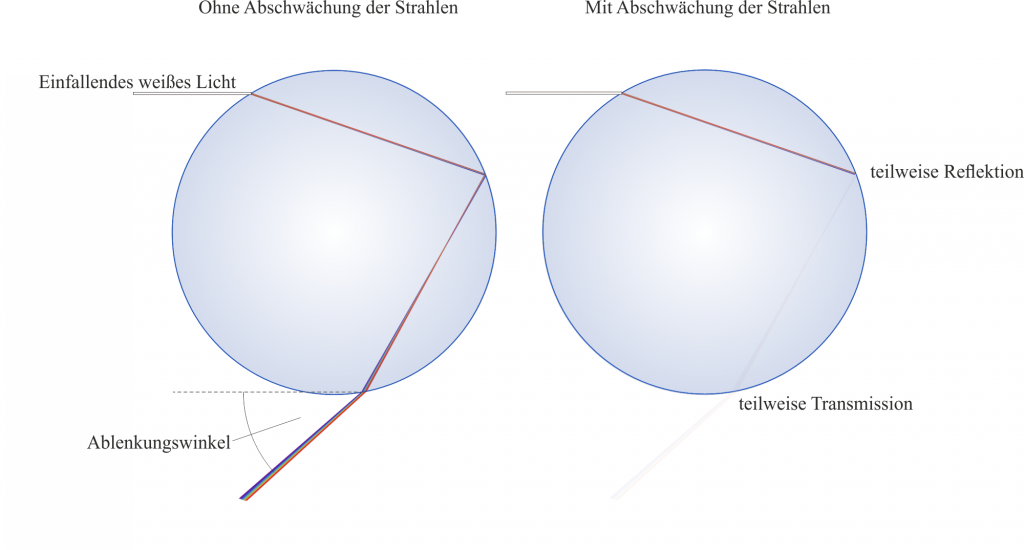
In der Abbildung oberhalb ist nun folgendes dargestellt: Der Lichtstrahl tritt in das als kugelförmig angenommene Wassertröpfchen ein. Aufgrund des Übergangs von einem optisch dünnerem Medium (Luft) in ein optisch dichteres Medium werden die Strahlen zunächst zum Lot gebrochen. Auf ihrem weiteren Pfad treffen sie dann wieder auf eine Grenzfläche – dort fallen sie mit einem Winkel kleiner als dem kritischen Winkel ein und nur ein geringer Bruchteil wird innerhalb des Tropfens reflektiert. An einem dritten Punkt schließlich treten sie aus dem Wassertropfen aus und werden fast in Richtung der Sonne zurückgeworfen. Wir sehen dass selbst ein Lichtstrahl der nur einmal innerhalb des Tropfens reflektiert wurde bereits stark abgeschwächt wird. Bei einer doppelten Reflektion wäre diese Abschwächung noch deutlicher.

Zusätzlich stellen wir fest, dass der ursprünglich weiße Lichtstrahl in seine Bestandteile aufgebrochen wurde. Aus dem Tropfen tritt ein Bündel farbiger Strahlen in leicht verschiedenen Winkeln aus. Blau wurde, insgesamt am stärksten abgelenkt, Rot hingegen am schwächsten.

Eine relative Intensitätsverteilung

Natürlich tritt aber nicht nur an einer Stelle Licht in den Tropfen ein. Sehen wir uns für Blaues Licht an was bei vielen verschiedenen Lichtstrahlen passiert:

Update 21.07.2019: Im Nachhinein betrachtet ist die obige Abbildung nicht wirklich gelungen da die Dichte der einfallenden Strahlen zu hoch gewählt ist. Könnte man noch einzelne Strahlen verfolgen wären die unten beschriebenen Dinge leichter zu sehen. So aber, und durch den Umstand, dass die einfallenden Strahlen von den Reflektierten überzeichnet werden, kann man eigentlich aus der Grafik so wie sie jetzt ist nur bedingt etwas lernen. Sollte ich die Zeit finden erstelle ich die Grafik neu.

Wir sehen, dass sich in einem bestimmten Ablenkungswinkelbereich die Strahlabschwächung anscheinend in Grenzen hält, in andere Bereiche jedoch kaum etwas zurückreflektiert wird. Können wir dies vielleicht noch etwas deutlicher zeigen und nebenbei herausfinden wo das Maximum liegt?

Zuerst ist interessant – gibt es einen maximalen Ablenkungswinkel? Und es stellt sich heraus – den gibt es. Er liegt für blaues Licht mit $470\;\text{nm}$ etwa bei $41.6^o$. Und noch etwas besonderes passiert bei diesem Winkel – in diesem Winkelbereich treten besonders viele Lichtstrahlen wieder aus dem Tropfen aus:

Das alleine reicht noch nicht ganz aus um sagen zu können in welchem Winkel das gebrochene Licht am hellsten ist. Wir müssen auch noch berücksichtigen wieviel Energie der Strahl auf seinem Weg durch den Tropfen verloren hat. Es könnte ja durchaus sein, dass alle Strahlen die bei ca. $41.6^o$ austreten beinahe ihre gesamte Energie abgegeben haben (Wir werden aber gleich feststellen, dass dies nicht so ist). Dafür verwenden wir die Reflektionskoeffizienten (bzw. Transmissionskoeffizienten) aus den Fresnellgleichungen.

Man kann nun eine relative Strahlungsintensität für jeden Ablenkungswinkelbereich berechnen welche uns sagt wo am meisten Licht hingebrochen wird, also anschaulich, ob zB. ein Beobachter im Bereich von $24.5^o – 25.5^o$ große Helligkeit sehen würde.

Siehe da, unterhalb von $20^o$ ist diese relative Strahlungsintensität sehr gering, erst ab diesem Winkel verlässt ein nennenswerter Bruchteil des Maximums den Tropfen. Das Maximum liegt für $470\;\text{nm}$ übrigens ca. bei $41.6^o$. Das sollte nicht ganz überraschend sein, denn dies ist der halbe Winkel unter dem einem Beobachter der blaue Bogen eines Regenbogens erscheint.

Fazit

Was haben wir gemacht? Zunächst einmal einen Wassertropfen als Sphäre angenähert. Dann haben wir mittels geometrischer Optik Strahlen betrachtet die

• in den Wassertropfen eintreten und dort
• einfache Reflektion erfahren und anschließend
• wieder austreten.

Wir haben Strahlen vernachlässigt die

• … direkt am Wassertropfen reflektiert werden bevor sie in diesen eintreten.
• … innerhalb des Tropfens mehrfach reflektiert werden.

Für die von uns betrachteten Strahlen konnten wir feststellen, dass

• … es einen maximalen Ausfallswinkel gibt. Konkret werden sie im sichtbaren Bereich also so gebrochen, dass sie alle in Richtung der Lichtquelle wieder aus dem Tropfen austreten. Der Winkel zwischen ursprünglichem Lichtstrahl und den Zurückreflektierten ist kleiner gleich diesem maximalen Winke.
• … die größte Strahlungsintensität beim maximalen Austrittswinkel vorgefunden wird
• … die Strahlungsintensität bei kleinen Ausfallswinkeln vernachlässigbar gering ist.

Mit der geometrischen Optik können wir also Regenbögen erklären, für die Glorie finden wir aber nichts was die starke Rückreflektion von Licht bei kleinen Ablenkungswinkeln beschreibt (also im Bereich von unter $10^o$ zum Beispiel).

Daraus können wir direkt folgern: Geometrische Optik allein kann Glorien nicht erklären! Es fehlt einfach die nötige Strahlungsintensität um den hellen Bereich erklären zu können.

Könnten nicht vielleicht doch noch Mehrfachreflektionen innerhalb des Tropfens die Erklärung liefern? Das scheint sehr unwahrscheinlich zu sein da ein Strahl um so stärker abgeschwächt er wird je mehr interne Reflektionen er erfährt. Verfolgt man diese Idee allerdings weiter findet man die Erklärung für Sekundärbogen eines Regenbogens – dieser wäre für blau bei etwa $54^o$ und entsteht durch Lichtstrahlen die innerhalb des Tropfens zweimal reflektiert werden. Der Glorie allerdings können wir so nicht näherkommen.

Tatsächlich brauchen wir dazu die Wellenoptik. Abhängig davon ob ich eine gute Möglichkeit finde dieses Erklärungsmodell darzustellen wird dies das Thema eines der nächsten Artikel werden.

Literatur

Glory formation – Surface waves and Debye Theor
The Optics of a Water Drop