Der Begriff radioaktive Strahlung geistert immer mal wieder durch die Medien – aber was versteht man eigentlich darunter? Da ich unlängst in den Besitz einiger Dosimeter (Strahlungsdosimeter, Satz, taktisch der Frieseke & Höpfner GmbH) gekommen bin dachte ich mir, dass dies eine gute Gelegenheit darstellt etwas darüber zu schreiben. In diesem Artikel wird es also darum gehen, was radioaktive Strahlung eigentlich ist. Ursprünglich wollte ich auch etwas ausführlicher über Messmethoden schreiben, konkret mit den oben abgebildeten Dosimetern. Aus verschiedenen Gründen, unter anderem der Artikellänge, wird das aber eventuell erst in einem Folgeartikel Platz finden. Hier gehts nun einfach darum, eine Idee zu bekommen, was es mit dieser ominösen radioaktiven Strahlung eigentlich auf sich hat.
Radioaktive Strahlung
Atome und ihr Aufbau
Ein großer Teil der Materie mit der wir im Alltag zu tun haben besteht aus Verbindungen von unzähligen Atomen. Von diesen Atomen gibt es verschiedene Arten, angefangen beim Wasserstoff, über Eisen bis hin zu exotischeren Varianten wie dem Einsteinium. Hier dringt es schon etwas durch: Abhängig davon wie ein Atom beschaffen ist handelt es sich um ein bestimmtes Element. Es lohnt sich daher einen kurzen Blick auf das Periodensystem der Elemente zu werfen – denn es kategorisiert diese Vielfalt.
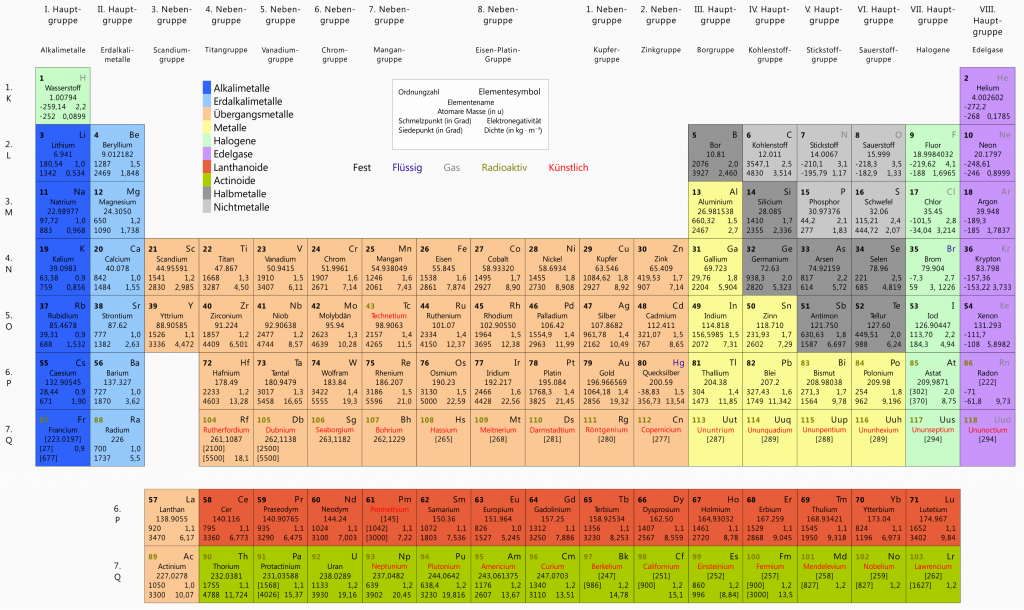
Wodurch unterscheiden sich nun alle diese Atome / Elemente? Tauchen wir etwas tiefer ein stellen wir fest, dass Atome zusammengesetzte Objekte sind. Sie können anschaulich in einen Kern und eine Hülle eingeteilt werden. Im Kern befinden sich Protonen und Neutronen, wobei erstere positiv geladen und letztere ladungslos sind. Die Hülle besteht aus negativ geladenen, viel leichteren Elektronen.
Ein beliebtes Bild zur Veranschaulichung ist hierbei ein auf dem Rutherfordschen Atommodell basierendes – jenes von den um den Kern kreisenden Elektronen. Dieses ist zwar aus verschiedenen Gründen unzureichend, aber um einen ersten Eindruck zu bekommen verwenden wir es dennoch, denn den groben Aufbau von Atomen gibt es korrekt wieder.
[expand title=“Warum das Rutherfordsche Atommodell nützlich aber unzureichend ist“]
Das Rutherfordsche Atommodel hat mehrere Probleme, das augenscheinlichste hat aber mit den kreisenden Elektronen zu tun. Ein Kreisförmige Bewegung ist eine beschleunigte Bewegung – die Elektronen müssen ständig ihre Bewegungsrichtung verändern damit sie um den Kern kreisen können!
Beschleunigte Ladungen (und das Elektron trägt ja eine Ladung) geben aber elektromagnetische Strahlung ab (zum Beispiel in Form von sogenannter Wärmestrahlung), und diese Abgabe von Strahlung bedeutet, dass die Elektronen ständig Energie verlieren würden. Dieser Energieverlust resultiert in immer geringerer Geschwindigkeit und damit einhergehenden engeren Kreisbahnen bis das Elektron schließlich in den Atomkern stürzt.
Das Rutherfordsche Atommodell kann also nicht beschreiben, weshalb die Materie stabil ist – ein sehr großes Defizit. Aber es liefert uns ein anschauliches Bild davon, aus wievielen Elektronen, Protonen und Neutronen ein Atom besteht und wo sich diese im Atom befinden.
Tatsächlich gab es später noch Adaptionen wie zum Beispiel das Bohrsche Atommodell. In diesem wurde postuliert, dass es gewisse optimale stabile Bahnen gibt auf welchen sich die Elektronen bewegen können ohne Energie zu verlieren. Diese Modell ermöglichte zwar unter anderem eine Vorhersage und Erklärung der Linienspektren von Atomen, stellte allerdings ebenfalls nur ein Hilfkonstrukt dar.
Für eine exakte Beschreibung muss die Quantenmechanik herangezogen werden (auch relativistische Effekte werden dabei berücksichtigt), allerdings ist diese für einen ersten Einstieg wohl nicht ganz so anschaulich. Letztlich werden dort für die Elektronen im Feld des Kerns nur mehr Aufenthaltswahrscheinlichkeiten angegeben.
[/expand]

Im Periodensystem sind die Atome nun der Ordnungszahl $Z$ entsprechend geordnet – diese gibt uns an wieviele Protonen sich im Kern befinden. Da Protonen einfach positiv geladen sind, verrät es uns auch gleich, wie stark er geladen ist, daher wird $Z$ auch Kernladungszahl genannt. Alle Atomkerne mit gleichem $Z$ sind also demselben Element zuzuordnen.
Für das oberhalb abgebildete Lithium Atom ist $Z_{\text{Li}}=3$ während für Gold $Z_{\text{Au}}=79$. Also hat Lithium $3$ Protonen im Kern, Gold dagegen schon $79$. Wie sieht es nun mit der Zahl der Neutronen $N$ aus, und hat auch diese – abgesehen vom Gewicht – einen Einfluss auf das Atom?
Für weitere Überlegungen ist es hilfreich ein weiteres Klassifikationsschema zu betrachten – die Nuklidkarte. Diese katalogisiert alle Varianten (Nuklide) eines Elements die auftreten können, und Variante bedeutet hierbei, dass die Neutronenzahl variiert. Der schwarze Block ganz links unten (besser sichtbar in der Vergrößerung) entspricht übrigens dem Element Wasserstoff.

Tatsächlich kann die Anzahl der Neutronen die sich in einem Atomkern befinden also variieren und zu Instabilitäten führen. Aber auch wenn der Kern groß genug ist gibt es für Elemente mit größerer Ordnungszahl einfach keine dauerhaft stabile Anordnung mehr . Dies ist zum Beispiel für $Z>82$ der Fall – in der Nuklidkarte daran erkennbar, dass oberhalb von Blei keine stabilen Elemente (schwarz eingefärbt) oder Isotope mehr existieren. In beiden Fällen kommt es aufgrund dieser Instabilitäten schließlich zu Zerfallsprozessen – und hier sind wir nun dort angelangt wo wir hinwollten. Radioaktiv ist ein Element dann, wenn sein Atomkern aufgrund seiner Konfiguration instabil ist, zerfällt, und dabei ionisierende Strahlung abgibt. Ionisierend bedeutet dabei, dass die Strahlung die Fähigkeit hat, anderen Atomen oder Molekülen Elektronen zu entreißen und somit mit einer elektrischen Ladung zurückzulassen.
Warum sind größere Atomkerne nicht mehr stabil?
Eigentlich müsste die Frage eher lauten, weshalb Atomkerne mit mehr als einem Proton überhaupt stabil sein können, und weshalb die Neutronen dort bleiben. Denn die Kraft die geladene Teilchen aufeinander ausüben wird beschrieben durch das Coulombsche Kraftgesetzt. Ladungen mit gleichem Vorzeichen stoßen sich ab: Positiv und Positiv, sowie Negativ und Negativ. Nur entgegengesetzte Ladungen ziehen sich an – Positiv und Negativ; und zwischen ungeladenen Neutronen wirkt keine Kraft. Warum also bleiben gerade im Kern Protonen so dicht beieinander und warum fliegen die Neutronen nicht einfach davon?
Grob gesagt liegt es daran, dass die Coulombkraft nicht die einzige ist die hier wirkt. Auf Distanzen wie jenen zwischen den im Atomkern befindlichen subatomaren Teilchen (Protonen und Neutronen) – etwa ein Femotometer $=10^{-15}\;\text{m}$ – wirkt die Kernkraft. Sie ist ein Überbleibsel der starken Wechselwirkung, einer der vier Grundkräfte in der Physik, und auf solch kurzen Abständen viel stärker als die Coulombkraft. Außerdem wirkt sie auch auf Neutronen.
Um so weiter man sich vom Kern entfernt, um so schneller fällt die Kernkraft im Vergleich zu letzter wieder ab, und bereits bei $2.5\;\text{fm}$ (Femtometern) sind beide etwa gleich stark. Also gibt es einen Bereich wo die durch die Kernkraft bedingte Anziehung zwischen den subatomaren Teilchen die Abstoßung durch die Coulombkraft überwiegt! Wenn aber der Kern wächst weil er aus immer mehr Protonen und Neutronen besteht, dann kommen die Abstände zwischen den Kernbestandteilen irgendwann in den Bereich, wo die Coulombkraft die Kernkraft schon beinahe aufwiegt. Und je näher der Kerndurchmesser dieser Grenze ist, desto weniger stabil ist der Kern. Die Grenze ist, wie wir der Nuklidkarte entnehmen können, bei $Z=83$ erreicht.
Aber warum komprimiert diese Kernkraft die subatomaren Teilchen nicht unendlich dicht wenn sie in diesem Bereich so stark anziehend wirkt? Das liegt daran, dass diese auf noch kürzeren Abständen ($<0.7\;\text{fm}$) abstoßend wirkt. Es gibt also einen schmalen Bereich in dem die Kernkraft anziehend wirkt und stärker als die abstoßende Wirkung der Coulombkraft ist. In diesem können sich stabile Kerne bilden.
Radioaktiver Zerfall
Nun werfen wir einen genaueren Blick auf die am häufigsten vorkommenden Zerfallsprozesse, was mit den ursprünglichen Atomkernen passiert und was für Zerfallsprodukte entstehen. In einem Fall entsteht hochenergetische elektromagnetische Strahlung während in den anderen geladene Teilchen abgegeben werden. Ein Überblick über weitere mögliche Zerfälle findet sich hier.
Diese Zerfallsprozesse werden klassisch in drei Kategorien eingeteilt – Alpha, Beta und Gamma – wobei sich die historische Einteilung danach richtet wie weit sich die jeweilige Strahlung in Materie ausbreiten kann.
Alpha Zerfall
Dies ist eine Zerfallsvariante in der ein Atomkern ein Gebilde bestehend aus zwei Neutronen und zwei Protonen abgibt. Dies entspricht einem Helium Atomkern und wird auch Alphateilchen genannt. Sehen wir uns dazu als Beispiel den Alphazerfall von Uran-238 an!
Zuallererst eine wichtige Frage – was wissen wir über dieses Element bzw. seine Zusammensetzung? Diese Informationen erhalten wir alle aus dem Periodensystem. Die Ordnungszahl ist $Z=92$ und die Massenzahl $A=238$. Die Differenz ergibt die Anzahl der Neutronen: $N=A-Z=146$. Somit können wir uns auch schon überlegen bzw. berechnen was passiert, wenn einem U-238 Kern plötzlich zwei Protonen und Neutronen verloren gehen.
Auf jeden Fall liegt ein neues Element vor, denn es bleiben nur mehr $90$ Protonen übrig. Im Periodensystem sehen wir, dass das Element mit Ordnungszahl 90 Thorium ist. Rechnerisch wissen wir nun auch, dass sich ich die Neutronenzahl auf $144$ reduziert hat und, dass somit die neue Massenzahl $90+144=234$ beträgt.
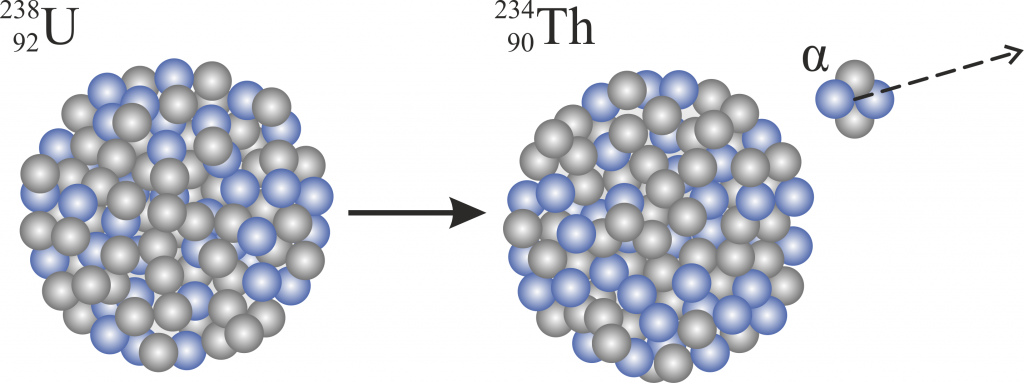
Kürzer angeschrieben:
\[\ce{^{238}_{92}U} \rightarrow \ce{^{234}_{90}Th} + \alpha\]
bzw. da wir ja wissen, dass das Alpha Teilchen einem Heliumkern entspricht
\[\ce{^{238}_{92}U} \rightarrow \ce{^{234}_{90}Th} + \ce{^{4}_{2}He^{2+}}\]
Das $2+$ rechts über dem Helium besagt nur, dass es zweifach positiv geladen ist. Normalerweise wird dies in dieser Art Gleichung allerdings nicht extra angegeben.
Eine spannende und unerwartete Anwendung von Alphazerfällen findet sich zum Beispiel in Rauchdetektoren. Diese beinhalten eine kleine Menge Americium welches geladenen Alphateilchen emittiert durch welche Luft in einer Ionisationszelle innerhalb des Detektors ionisiert wird. Dies bewirkt einen kleinen Stromfluss, denn Strom ist nichts anderes als Ladung die sich von einem Ort zum anderen bewegt (Ladung pro Zeit). Tritt nun Rauch in diese Zelle ein verringert sich dieser Fluss. Wird ein Abfall des Stroms festgestellt löst dies einen Alarm aus.
Von allen Strahlungsarten lässt sich die sogenannte Alphastrahlung am leichtesten abblocken. Dazu ist weder ein Bleianzug notwendig, noch eine besonders dicke Betonwand – ein Blatt Papier oder einige Zentimeter Luft reichen vollkommen aus. Aber nicht nur das, solange eine Strahlungsquelle tatsächlich nur Alphateilchen emittiert genügt auch die Schicht toter Hautzellen jedes Menschen, die Epidermis. Das Verschlucken eines Alphastrahlers wäre allerdings gefährlich.
Beta Zerfall
Der Beta Zerfall unterteilt sich eigentlich nochmals in zwei Untervarianten – den $\beta^-$ und den $\beta^+$ Zerfall. In ersterem Fall besitzt ein Atomkern einen Überschuss an Neutronen, in zweiterem einen an Protonen und der überschüssige Bestandteil zerfällt. Die entsprechenden Prozesse sehen so aus:
Beta-
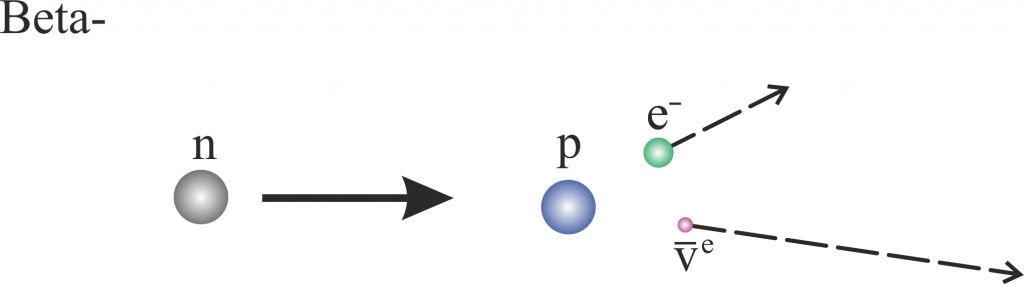
\[ \ce{n} \rightarrow \ce{p}+\ce{e^-}+\ce{\bar{v}}_e \]
Hier zerfällt das „überschüssige“ Neutron $\ce{n}$ in ein Proton $p$, Elektron $e^-$ und ein Antineutrino $\ce{\bar{v}}_e$, wohingegen beim $\beta^+$ Zerfall
Beta+
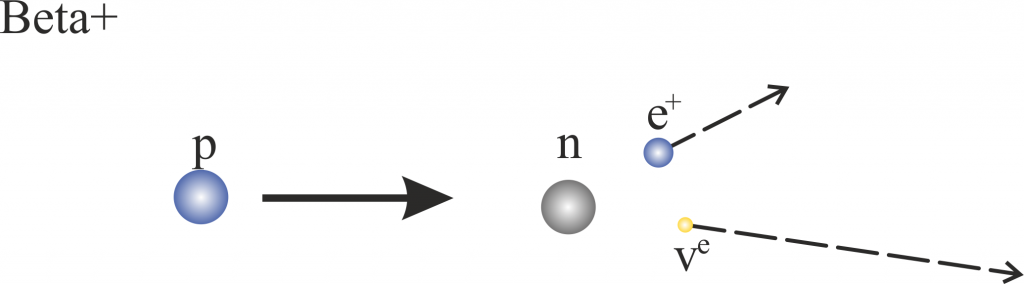
\[ \ce{p} \rightarrow \ce{n}+\ce{e^+} + \text{v}_e \]
das Proton in ein Neutron, Positron $\ce{e^+}$ und ein Neutrino $\text{v}_e$ zerfällt. Freie Protonen (also welche die nicht in einem Kern gebunden sind) sind allerdings stabil – bislang konnte noch kein solcher Zerfall eines freien Protons beobachtet werden.
Sieht man sich beide Zerfälle an stellt man noch etwas fest: Die Ladung bleibt erhalten! Zerfällt ein Neutron ergibt die Summe der Ladungen der Zerfallsprodukte ebenfalls wieder $0$, beim Zerfall eines Protons beläuft sich diese Summe aus diesem Grund aber auf $+1$ (da das Proton, bezogen auf die Elementarladung, einfach positiv geladen ist ).
Die Elektronen bzw. Positronen der Betastrahlung dringen bereits tiefer in Materialien ein. Um sie aufzuhalten wären bereits zentimeterstarke Barrieren notwendig. Neutrinos und Antineutrinos hingegen sind dafür bekannt sich nicht allzuviel um Materie zu kümmern. Sie fliegen grundsätzlich durch fast alles durch und interagieren nur sehr schwach (dazu im nächsten Abschnitt etwas mehr).
Eine kurze Geschichte zu Erhaltungsgrößen und Vorhersagen
Erhaltungsgrößen wie zum Beispiel Energie, Impuls und Drehimpuls nehmen in der Physik eine wichtige Rolle ein. Sie ermöglichen es unter anderem fundamentale Aussagen über das Verhalten von eventuell nur aufwändig beschreibbaren Systeme zu machen. Lässt man einen Stein vom Dach eines Hauses fallen kann rein aus Fallhöhe $h$ und Kenntnis der Schwerebeschleunigung der Erde $g$ die maximal erreichbare Geschwindigkeit beim Aufschlag abgeschätzt werden. Natürlich könnte man auch die Bewegungsgleichungen aufstellen und diese lösen, allerdings ist dies bereits merkbar aufwändiger als einfach $v_\text{max}=\sqrt{2gh}$ zu berechnen. Klarerweise wird der Stein $v_\text{max}$ nur im Vakuum erreichen, aber schon allein die Möglichkeit eine Obergrenze angeben zu können ist eine sehr nützliche (aber bei weitem nicht die einzige) Anwendung von Erhaltungssätzen. Zurück zur eigentlichen Geschichte.
Ursprünglich konnten Neutrinos nicht detektiert werden da diese nur sehr schwach mit Materie wechselwirken. So passieren von der Sonne kommend in etwa 60 Milliarden dieser Teilchen jede Sekunde eine Fläche die ca. so groß ist wie ein Daumennagel ($1\;\text{cm}^2$) (Bahcall 2004). Da man Neutrinos nicht detektieren konnte schien es bei seiner Entdeckung also so, als ob der Beta- Zerfall unter anderem die Energieerhaltung verletzte. In einem Brief vermutete 1930 schließlich der Physiker und spätere Nobelpreisträger Wolfgang Pauli, dass ein zusätzliches Teilchen mit bestimmten Eigenschaften diese scheinbare Diskrepanz erklären könnte. Er sollte recht behalten: 26 Jahre später konnte das Elektron Neutrino experimentell nachgewiesen werden.
Gamma Zerfall
Nach einem Alpha oder Beta Zerfall bleibt das Atom in einem angeregten Zustand. Wenn es von diesem schließlich innerhalb kurzer Zeit in einen Zustand niedrigerer Energie fällt wird dabei ein Photon abgegeben dessen Energie der Energiedifferenz des ursprünglichen und des neuen Zustandes entspricht – in den hier betrachteten Fällen ist diese sehr hoch!
Sehen wir uns das am Fall des $\ce{^{60}_{27}Co}$ Zerfalls an. Dieses Kobalt Isotop erfährt Beta- Zerfall welcher mit der Emission von hochenergetischen Photonen (Gammastrahlung) einhergeht:
\[ \ce{^{60}_{27}Co} \rightarrow \ce{^{60}_{28}Ni} + \ce{e^-} + \ce{\bar{v}}_e + \gamma_1 + \gamma_2 \]
Ein Neutron des Kerns zerfällt also. Das so entstandene Proton bleibt im Kern gefangen – daher wird aus Kobalt Nickel – während sich Elektron und Neutrino gemeinsam aus dem Staub machen. Da sich das ursprüngliche Atom danach in einem angeregten Zustand befindet fällt es aus diesem in zwei Schritten auf einen „unangeregten“ Zustand hinunter. Bei jedem dieser Schritte wird ein Photon hoher Energie abgegeben welche in obiger Gleichung durch $\gamma_1$ und $\gamma_2$ angedeutet wurden. Diese haben Energien von $1.17\text{MeV}$ und $1.33\text{MeV}$, im Vergleich dazu nimmt sich sichtbares Licht mit höchstens von $3.2\text{eV}$ äußerst bescheiden aus – das ist fast ein Faktor $10^6$ weniger!
Kann man sich den Energieunterschied noch irgendwie anschaulich vorstellen? Naja, stellen wir uns einen Kampfjet vor der in etwa eine Höchstgeschwindigkeit von Mach 3 schafft. Dies entspricht $1021\text{m/s}=3680\text{km/h}$. Zum Vergleich: ein Eurofighter schafft anscheinend eine Höchstgeschwindigkeit von ca. Mach 2. Das Verhältnis der Energie von sichtbarem Licht zu Gammastrahlen ist in etwa das gleiche wie das der kinetischen Energie eines gemütlich mit $1\text{m/s}$ rollenden Kampfjets im Vergleich zum Flug desselben mit Mach 3.
Gammastrahlung ist auch die am aufwändigsten abzuschwächende Art der Strahlung – dicke Schichten aus Materialien hoher Dichte sind hierfür notwendig (zum Beispiel Blei).
Ein kurzer Überblick
Jedenfalls fassen wir der Übersicht halber die hier besprochenen Zerfallsprozesse und ihre Produkte in einer Tabelle zusammen:
| Zerfall | Produkt | Typ |
|---|---|---|
| Alpha | $\ce{^{4}_{2}He^{2+}}$ | Teilchen |
| Beta - | $\ce{p}+\ce{e^-}+\ce{\bar{v}}_e$ | Teilchen |
| Beta + | $\ce{n}+\ce{e^+} + \text{v}_e$ | Teilchen |
| Gamma | hochenergetisches Photon | EM-Strahlung |
Zusammenfassung
Jetzt haben wir eine Idee davon was es mit den häufigsten Zerfallsarten auf sich hat und was für Produkte dabei entstehen. Im Fall von Alpha- und Betazerfall bleiben uns positiv oder negativ geladene Teilchen mit zum Teil hohen kinetischen Energien, im Fall von Gamma Zerfall hochenergetische Photonen.
Alle drei Varianten können Materie mit der sie interagieren auf verschiedenen Wegen ionisieren, also Elektronen aus anderen Atomen lösen. Photonen benötigen hierzu allerdings eine gewisse Mindestenergie die bereits mit kurzwelliger UV-Strahlung bzw. Licht mit Wellenlängen unterhalb von $121\;\text{nm}$ erreicht wird. Dabei gilt: Je kurzwelliger desto höher die Energie.
Dies liefert uns auch den entscheidenden Hinweis darauf wie wir feststellen können ob in unserer Nähe etwas zerfällt, oder besser gesagt, etwas mehr zerfällt als normalerweise üblich. Denn radioaktiver Zerfall findet im Prinzip immer und überall statt – ein guter Teil der natürlichen Hintergrundstrahlung entsteht durch das in der Luft vorhandene Gas Radon.
Im Endeffekt läuft es darauf hinaus festzustellen, ob wir einen durch die Ionisation bedingten Ladungstransfer feststellen können. Eine Möglichkeit dies zu bewerkstelligen haben wir bereits beim Alpha Zerfall kennengelernt – die Messung des Stromflusses beim Rauchdetektor durch eine Ionisationskammer.
Danke fürs lesen und wie üblich – bei Fragen, Kritik oder Unklarheiten einfach was posten.
Literatur
Effects of Radiation on Matter – chemWiki der UC Davis
Bahcall J., Serenelli A., Basu S. – New solar opacities, abundances, helioseismology, and neutrino fluxes, arXiv:astro-ph/0412440v3, 2014



