Vor ca. einer Woche wurde ein, wie ich finde, recht interessantes Paper publiziert. In dieser Studie wurde eine Methode vorgestellt mit der Schriftrollen die beim Ausbruch des Vesuvs im Jahr 79 verkohlt (carbonized) wurden lesbar gemacht werden können. Das Lesbarmachen geschah zwar auch bisher schon. Allerdings musste man dazu die Schriftrollen aufrollen, und aufgrund des recht fragilen Zustandes ist dies nicht zerstörungsfrei möglich. Also keine zweiten Versuche. Um die Rollen jedoch auch für die Zukunft zu erhalten, sucht und entwickelt man aber neue Methoden – so wie zum Beispiel eine gerade vorgestellte welcher ich diesen Beitrag widmen möchte.
Im Prinzip hätte man gerne sowas wie im Fall der Röntgentomographie bzw. Computertomographie (im Folgenden kurz RT bzw. CT). Man würde also gern durch ein undurchsichtiges Material durchsehen und darunterliegende Strukturen erkennen. Mit RT/CT funktioniert das aber nicht ganz, und um zu verstehen weshalb überlegen wir uns kurz wie ein Röntgenbild eigentlich gemacht wird bzw. was wir eigentlich sehen wenn wir eines betrachten.
Röntgenbilder
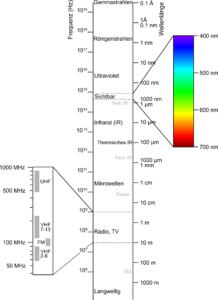
Zunächst benötigt man eine Quelle für Röntgenstrahlen. Das Phänomen das man sich zu Nutze macht ist die sogenannte Bremsstrahlung. Elektronen werden durch eine angelegte Spannung auf eine hohe Geschwindigkeit beschleunigt und schlagen dann auf ein Ziel auf. Werden Ladungen nun stark beschleunigt (oder wie hier eben stark entschleunigt) geben diese elektromagnetische Strahlung ab. Im Fall von Röntgenröhren ist dies die namensgebende Röntgenstrahlung deren Wellenlängen im elektromagnetischen Spektrum im Pikometerbereich liegen. Welche Eigenschaften diese Strahlung hat erläutern wir in der folgenden Klappbox etwas genauer (ohne groß auf Formeln zurückzugreifen).
[expand title=“Eigenschaften der Röntgenstrahlung“]
Für unsere Röntgenstrahlenquelle gibt es in Form einer einfachen Gleichung (gegeben durch das Duane-Hunt Gesetz) eine Möglichkeit mit der die auf diese Weise minimal erreichbare Wellenlänge angegeben werden kann:
\[ \lambda_\text{min} = \frac{hc}{eU} \]
Rechnen wir mit einer Spannung von $U = 60\text{kV}$ ergibt sich mit $e$ der Ladung des Elektrons, $h$ dem Planck’schen Wirkungsquantum und $c$ der Lichtgeschwindigkeit eine minimal erreichbare Wellenlänge von $\lambda_\text{min}=24.8 \text{pm}$. Damit liegen wir erwartungsgemäß schon gut im Bereich der Röntgenstrahlung. Zum Vergleich: Sichtbares Licht hat Wellenlängen zwischen ca. $400\text{nm}$ bis $700\text{nm}$.
Die Leistung $P$ welche dann von einer derart gebremsten Ladung insgesamt abgegeben wird kann ebenfalls berechnet werden – und zwar mit der Lamor Gleichung. Tatsächlich müssen wir für typische Röntgenrören Spannungen bereits auf deren relativistische Vergallgemeinerung zurückgreifen.
[/expand]
Die so erzeugte Strahlung lässt man nun mit einer bestimmten Fokussierung auf das im sichtbaren Spektrum undurchsichtige Objekt von Interesse auftreffen. Hinter dem Objekt befindet sich schließlich ein Detektor. Das kann ein Röntgenfilm sein oder aber auch – wie in modernen Geräten – ein szintillationsbasierter Detektor. Letzteres bedeutet, dass ein Material verwendet wird welches, wenn ein Röntgenphoton auftrifft, dieses absorbiert, und die so gewonnene Energie in Form von Licht längerer Wellenlänge wieder abgibt (Szintillation). Dieses Licht kann schließlich, zum Beispiel mit einer Photodiode, detektiert werden und die an dieser gemessene Spannung steht dann in Zusammenhang mit der Intensität des durch die Probe durchgetretenen Röntgenlichts. Im Fall des Röntgenfilms ist das ganze etwas anschaulicher: Je mehr Röntgehnstrahlung durch die Probe transmittiert wird, desto dunkler erscheint die jeweilige – ursprünglich weiße – Stelle am Film.
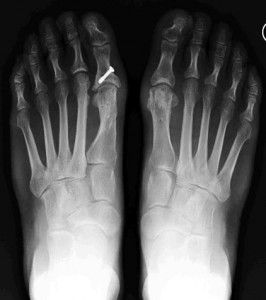
Quelle Autor: Personalo unter CC-BY-SA-3.0
Und damit haben wir das Prinzip hinter der Röntgen-/Computertomographie entdeckt. Wir können zwar ins Innere jedes Objektes blicken welches ausreichend durchlässig für Röntgenstrahlung ist, aber ein brauchbares Bild erhalten wir nur dann, wenn die Beschaffenheit der Probe so ist, dass ausreichend Unterschiede in der Durchlässigkeit vorliegen. Wenn alles gleich gut transmittiert, dann erhalten wir ein Röntgenbild in einem gleichmäßigen Grauton. Befinden sich jedoch innerhalb der Probe Dinge, die einen Teil der Röntgenstrahlung blockieren, werden diese Stellen auf dem Bild heller wirken. Wir erhalten also ein kontrastreicheres Bild.
Und genau da stoßen wir auch auf das Problem mit RT/CT Verfahren wenn es um diese Schriftrollen geht. Einerseits wurde das ursprünglich organische Papyrus verkohlt. Andererseits war die „Tinte“ mit der auf diese geschrieben wurde schwarz und basierte auf Kohlenstoff (Mocella 2015). Beides hat eine sehr ähnliche Dichte und lässt Röntgenstrahlung ähnlich gut passieren – da lässt sich nicht viel erkennen.
Phasenkontrast Röntgenbildgebung
Zum Glück gibt es andere Methoden auf die wir in diesem Fall zurückgreifen können! Und, dass diese auch prinzipiell auf eingerollte Schriftrollen angewendet werden kann, das wurde im Eingangs zitierten Paper erstmals gezeigt. Die Idee hierbei ist nun auf eine andere Eigenschaft von elektromagnetischen Wellen zurückzugreifen – ihre Phase.
Was das genau ist, darauf kommen wir noch zurück. Beginnen wir erstmal mit folgender Fragestellung: Was passiert eigentlich, wenn einfarbiges Licht durch ein Medium transmittiert wird. Das Medium kann dabei eine Glasplatte sein welche zum Beispiel von grünem Licht durchdrungen wird, oder aber auch Gewebe das von einem Röntgenstrahl bestimmter Wellenlänge durchquert wird.

In obiger Abbildung sehen wir im Prinzip drei Bereiche. Luft, ein Medium und wieder Luft, wobei wir annehmen, dass das einfarbige Licht von Luft nicht beeinflusst wird (also vollständig transparent ist), und das Medium dafür teilweise durchlässig ist. Licht selbst ist eine elektromagnetische Welle und bewegt sich (in unserem Beispiel) von links auf das Medium zu. Das elektrisches Feld (bzw. dessen Realteil) habe ich eingezeichnet. Überlegen wir nun also was mit dem E-Feld während dieses Vorgangs geschieht – wobei wir uns auf die Effekte beschränken welche später für uns wichtig sind.
Zunächst trifft die Welle auf das Medium auf und wird dabei teilweise reflektiert und zu einem Teil transmittiert. Das E-Feld wird innerhalb des Mediums dann etwas abgeschwächt, ein bisschen Energie geht also an das Medium „verloren“, zusätzlich kommt es zu einem Phasenschub. Nichts anderes passiert auch bei Glasfenstern, auch diese absorbieren einen Teil des Sonnenlichts.
Schließlich erreicht die Welle das Ende des Mediums. Dort wird wieder ein Teil zurückreflektiert während der Rest daraus austritt. Das E-Feld wurde während dieses Prozesses einerseits abgeschwächt, andererseits hat es einen Phasenschub erhalten – relativ dazu wie das ursprüngliche E-Feld aussah. Die folgende Grafik soll uns dabei behilflich sein eine Idee zu bekommen, was dieser Phasenschub denn ist ($\Delta \phi$ kennzeichnet dessen Ausmaß).

Wir sehen also, dass die transmittierte Welle etwas zurückfällt. Das sechste eingezeichnete Minimum der transmittierten Welle liegt $\Delta \phi$ hinter dem sechsten Minimum der ursprünglichen Welle. Im Prinzip könnten wir auch andere Stellen vergleichen, wichtig ist nur, dass wir immer „dieselben“ vergleichen (also bei beiden den Abstand zwischen den Maxima ODER zwischen den Nulldurchgänge, etc.)
RT/CT greift rein darauf zurück, dass die Intensität der EM-Welle nach dem Durchtritt durch den Probanden abgenommen hat – und, dass die Materialien aus denen der Proband besteht die Intensität der Welle unterschiedlich verringern. Wenn diese Unterschiede – wie im Fall der Schriftrollen – nicht groß sind dann ist allerdings wenig zu erkennen.
Phasenkontrastbildgebung (PKB) kann jedoch aus dem Phasenschub noch Informationen über die Zusammensetzung des Mediums gewinnen. Das zugrundeliegende Prinzip ist, dass der Phasenschub davon abhängt, was der Röntgenstrahlung auf dem Weg durchs Medium so passiert. Genauer gesagt von den optischen Eigenschaften der Materialien und wie groß die darin zurückgelegte Strecke ist. Man hat anschließend verschiedene Möglichkeiten wie man diesen Phasenschub tatsächlich vermisst, auf die werde ich an dieser Stelle aber nicht eingehen.
Letztlich ermöglicht es diese Technologie auch, zweitausend Jahre alte, eingerollte und verkohlte Schriftrollen Schritt für Schritt entziffern zu können. Und trotz dieser Technik ist das keine leichte Aufgabe, wie auch die Autoren schreiben.
Der große Druck des pyroklastischen Materials hat die Schriftrolle komprimiert und die ursprüngliche interne Spiralstruktur deformiert. Das ergab eine nahezu chaotische Verwicklung und Faltung. Zusätzlich kleben die Windungen an manchen Stellen auch noch aneinander. All das führt dazu, dass die Buchstaben mehr oder weniger verzerrt sind.
Übersetzung von mir aus Mocella 2015. Das Problem liegt jetzt darin, dass mit PKB das Material Ebene für Ebene vermessen wird. Man hat also Ebene Flächen die quasi einen Schnitt durch die Schriftrolle repräsentieren, aber die Buchstaben sind nicht parallel dazu orientiert. Das macht – wie die Autoren selber sagen – die Analyse der Daten zu einer Herausforderung. Nichtsdestotrotz konnten einige Wörter entdeckt werden!

Für mich war das ein sehr faszinierendes Paper. Einerseits gab es mir die Möglichkeit mich ein bisschen mit Röntgentechnologien zu beschäftigen. Andererseits gibt es Schriftrollen die vor zweitausend Jahren verfasst wurden und von pyroklastischem Material verkohlt und verformt wurden. Und jetzt verwendet man aktuelle Technologie um etwas zu entziffern, das zwar immer da aber eben unzugänglich war. Die Autoren der Studie sind optimistisch, dass die Technik verbessert werden kann und damit letztlich Schriftrollen vollständig entziffert werden können. Und dann kann es möglich sein, dass bisher unbekannte oder vielleicht sogar verschollen geglaubte philophische Werke die sich in der „Villa dei Papiri“ befanden als sie vor 2000 Jahren von einem Strom pyroklastischen Materials überdeckt wurde, wieder lesbar gemacht werden. Großartige Aussichten!
Literatur
Mocella, V., et al. (2015) Revealing Letters in Rolled Herculaneum Papyri by X-Ray Phase-Contrast Imaging, Nat Commun 6.


2 Kommentare