Nebensonnen und wie sie entstehen

Dieses Phänomen ist mir vor nicht allzu langer Zeit bei einer längeren Autofahrt untergekommen. Bessere Fotos als meines sind unter anderem auf Wikipedia zu finden. Ich wusste zwar, dass es verschiedene Arten von Halos und Lichterscheinungen um die Sonne gibt, gesehen hatte ich jedoch noch keine(n). Als nächstes wollte ich dann wissen, wie solche Erscheinungen zustande kommen und nach kurzer Recherche bin ich auch fündig geworden. Und das wird Thema dieses Beitrags sein.

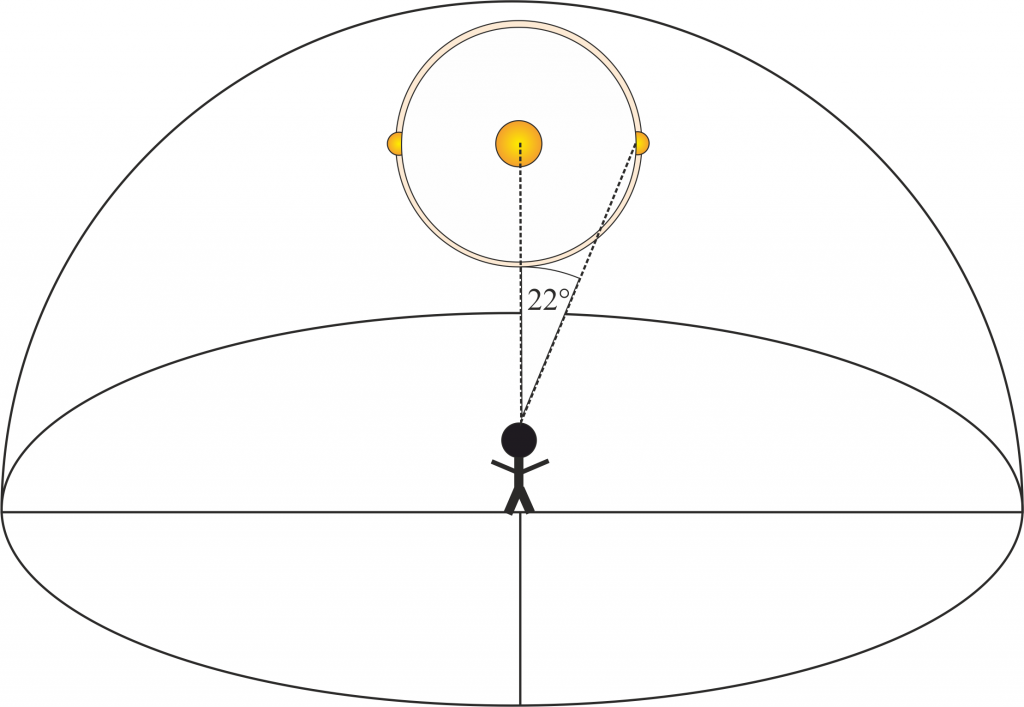
Grundsätzlich hat eine Nebensonne (auch Parhelion) eine Gemeinsamkeit mit einem 22° Halo wie er im nächsten Bild zu sehen ist:

Warum aber eigentlich 22° Halo? Sieht man diesen Ring am Himmel und hat man ein Winkelmessgerät zur Hand (auch mit einem Geodreieck nachmessbar) erscheint er dem Beobachter genau diesen Winkel von der Sonne entfernt.

Die Ursache für diesen Lichtring sind jedenfalls kleine plättchenförmige sechseckige Eiskristalle in der Atmosphäre.

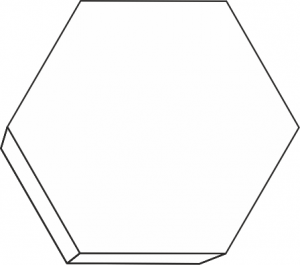
Stellen wir uns vor, dass wir uns einen Teil der Eiskristalle innerhalb des 22° Ringes und innerhalb der Nebensonne ansehen können. Was werden wir sehen?

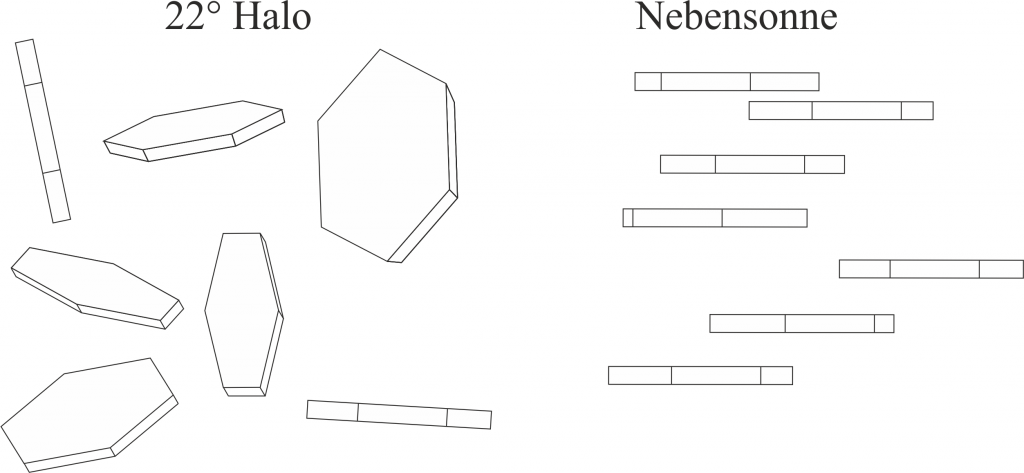
Im Fall eines kompletten 22° Ringes um die Sonne sind diese zufällig im Raum orientiert. Das bedeutet, dass ihre Grundfläche nicht bevorzugt in eine bestimmte Richtung ausgerichtet vorkommt. Damit haben wir auch den Unterschied zu den Nebensonnen entdeckt. Die Eiskristalle sind mit ihrer Grundfläche parallel zum Erdboden orientiert! Diese gleichmäßige Ausrichtung kommt durch den Bernoulli Effekt zustande. In diesem Beitrag möchte ich aber den Schwerpunkt auf die Brechung des Lichtes legen, daher gehe ich an dieser Stelle nicht weiter darauf ein.

Jetzt wissen wir was in der Atmosphäre (abgesehen von Luft) vorhanden ist (die Eiskristallplättchen) und wie es orientiert ist (parallel zum Boden). Wie können wir uns jetzt überlegen, was mit dem Licht passiert, das auf ein solches Hexagon auftrifft?

Snelliussches Brechungsgesetz

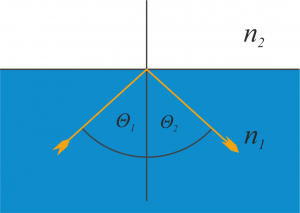
Unsere erste Station ist das Brechungsgesetz von Snellius, und dazu gleich eine Grafik mit Erklärung im Anschluss. Das Gesetz beschreibt, was passiert wenn ein Lichtstrahl welcher sich in einem Medium ausbreitet in einem bestimmten Winkel auf eine Oberfläche auftrifft und in das darunterliegende Medium eintritt.

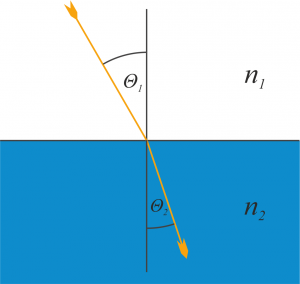
Beim Übergang von einem Medium mit Brechungsindex $n_1$ zu einem Medium mit größerem Brechungsindex $n_2$ wird ein Strahl der zum Lot im Winkel $\theta_1$ einfällt im Winkel $\theta_2$ in das zweite Medium eintreten. Er wird sozusagen zum Lot hin gebrochen. Wir können dem Strahl auch in die andere Richtung folgen. Dann hätten wir einen Strahl welcher innerhalb eines optisch dichteren Mediums im Winkel $\theta_2$ an der Grenzfläche eintrifft und im Winkel $\theta_1$ vom Lot weg gebrochen wird. Formal ist der Zusammenhang durch

\[ n_1 \sin{\theta_1} = n_2 \sin{\theta_2}\]

gegeben. Der Brechungsindex wird in der ausklappbaren Box unterhalb erklärt.

[expand title=“Was ist der Brechungsindex?“]

Licht breitet sich nur im Vakuum mit Lichtgeschwindigkeit aus. In anderen Medien wird es von Atomen absorbiert und wieder emittiert und durch die Verzögerung zwischen diesen beiden Vorgängen ergibt sich effektiv eine Verlangsamung.

Um dies zu beschreiben bedient man sich des Brechungsindexes $n$:

\[n = \frac{c_\text{Vakuum}}{c_\text{Medium}} \]

Dieser ist das Verhältnis von der Lichtgeschwindigkeit im Vakuum zur Lichtgeschwindigkeit im Medium – und somit größer als $1$. Tatsächlich hängt $c_\text{Medium}$ auch noch von der Wellenlänge ab – blaues Licht wird stärker verlangsamt als rotes Licht und somit stärker gebrochen. Auch gibt es noch weitere Abhängigkeiten, wir bleiben jedoch im Rahmen dieses Artikels bei obiger Vereinfachung da sie für den betrachteten Fall ausreichend ist.

Für Luft ist $n\approx 1$ und für Eis nehmen wir näherungsweise $n\approx1.31$ an.

[/expand]

Im Prinzip ist das auch schon das einzige physikalische Gesetz das wir berücksichtigen müssen. Allerdings ergibt sich für den Übergang von dichterem zu dünnerem Medium (zum Beispiel wenn ein Lichtstrahl im Wasser auf die Grenzfläche zwischen Wasser und Luft trifft) ein Sonderfall. Die totale Reflektion.

Totale Reflektion

Dieses Phänomen, das beim Übergang von einem Medium mit höherem Brechungsindex zu einem Medium mit niedrigerem auftreten kann, wird zum Beispiel beim Lichtwellenleitern  ausgenutzt. Hierbei ist der Einfallswinkel des Lichtstrahls größer als ein gewisser kritischer Winkel. Der Strahl kann daher nicht in das andere Medium übergehen sondern wird an der Grenzfläche reflektiert mit $\theta_2 = \theta_1$.

Wie groß dieser kritische Winkel $\theta_C$ ist kann man sich herleiten, siehe dazu die nächste ausklappbare Box. Er kann folgendermaßen berechnet werden:

\[ \theta_C = \arcsin{\frac{n_2}{n_1}} \]

[expand title = „Wie kommt man auf den kritischen Winkel?“]

Hierzu ziehen wir wieder das Snelliussche Brechungsgesetz heran und überlegen uns, ab welchem Einfallswinkel $\theta_1$ denn der Ausfallswinkel $\theta_2=90^o=\pi/2$ wird.

\[ n_1 \sin{\theta_1} = n_2 \sin{\pi/2} = n_2 \]

Das lässt sich direkt umformen und somit ist

\[\theta_C = \arcsin{\frac{n_2}{n_1}} \]

Für einen Lichstrahl im Eis der auf die Grenzfläche zur Luft trifft ist $\theta_C=49.8^o$

[/expand]

Herleitung mit grundsätzlichen Überlegungen

Jetzt kennen wir die notwendige Physik. Wenden wir sie also auf das Problem an!

Mit einem kleinen „Trick“ lässt sich sogar eine einfache Antwort auf die Frage geben, wie sich ein Lichtstrahl verhält der auf den Eiskristall auftrifft.  Die obere Hälfte des Hexagonplättchens hat nämlich – bis auf die fehlende Spitze – dieselbe Form wie ein Dispersionsprisma mit einem Winkel von $\epsilon = 60^o$.

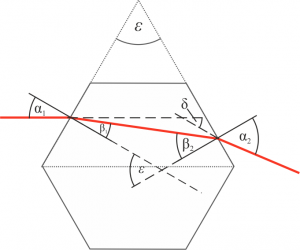
Hier sind nun relative viele Winkel eingezeichnet – sie sollen aber nur eines zeigen. Alles was getan werden muss um herauszufinden, wie ein Strahl der mit dem Winkel $\alpha_1$ einfällt abgelenkt wird, ist das Snelliussche Brechungsgesetz Schritt für Schritt anzuwenden bis man einen Ausdruck für $\alpha_2$ erhält.

Zu unserem Glück wurde das für Prismen aber schon durchgeführt. Man kann sogar angeben, um welchen Winkel $\delta_\text{minimal}$ die Ablenkung mindestens erfolgt. Wenn wir diesen ermitteln können, sollte uns das einen Eindruck davon vermitteln wie weit die Nebensonne von der Sonne entfernt sein müsste. Die entsprechende Gleichung lautet:

\[ \delta_\text{minimal} = 2 \arcsin{ \left( n \sin{\left( \epsilon/2 \right) } \right) }- \epsilon \]

und eine Herleitung findet sich zum Beispiel hier.

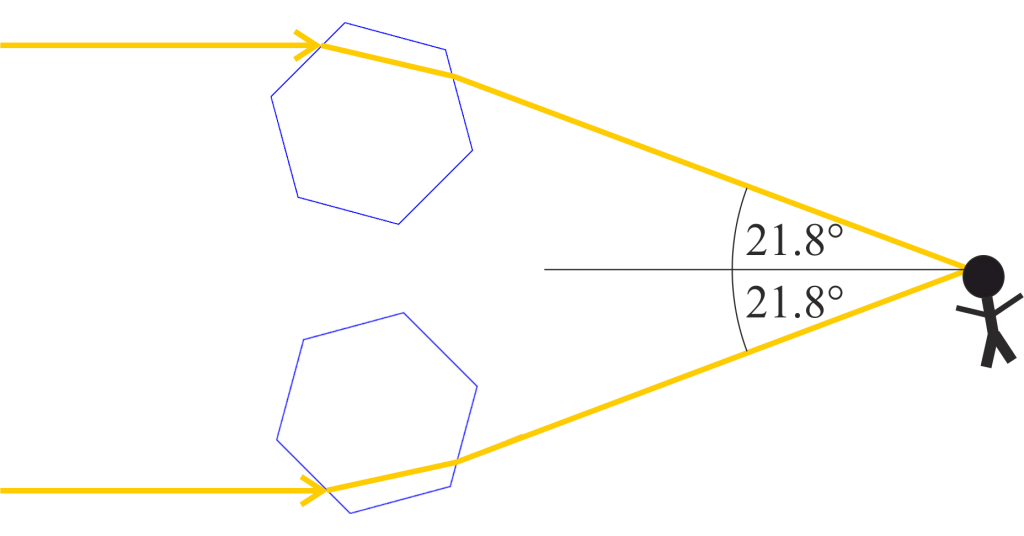
Nun setzen wir Werte ein. Der Winkel $\epsilon$ beträgt $60^o$ und der Brechungsindex eines Eiskristalles im Fall von gelb-orangen Licht mit $\lambda=589\text{nm}$ ist $n\approx1.31$. Es ist mit diesen Werten

\[ \delta_\text{minimal} = 21.8^o \]

Der $22^o$ Halo kann – für diese Wellenlänge – tatsächlich also schon bei $21.8^o$ beginnen.

Simulation mit dem PC

Ich wollte das ganze auch noch auf eine andere Art und Weise auswerten. Und zwar hat mich interessiert, welcher Anteil vom Sonnenlicht in welche Richtung abgelenkt wird. Davon ausgehend, dass zwar alle sechseckigen Eiskristalle parallel zum Boden ausgerichtet sind, aber man ja nicht unbedingt weiß wie sie sonst orientiert sind. Also habe ich für ein Hexagon simuliert was passiert, wenn das Licht in verschiedenen Winkeln darauf auftrifft.

Um dies zu simulieren habe ich das Sechseck Schritt für Schritt gedreht und für jeden Winkel die Berechnung laufen lassen. Das habe ich so oft wiederholt, bis das Sechseck wieder genauso ausgerichtet war wie am Anfang. Das GIF unterhalb zeigt den Ablauf.

Das Programm habe ich zusätzlich noch jeden Lichtstrahl der in eine bestimmte Richtung abgelenkt wurde zählen lassen. Dh. insgesamt wurden zB.: 0 Strahlen in den Bereich zwischen $11.5^o$ und $12.5^o$ abgelenkt, oder aber 1000 in den Bereich zwischen $23.5^o$ bis $24.5^o$.Natürlich werden manche Strahlen auch gar nicht abgelenkt. Ein paar Beispiele sind in der Folgenden Grafik gezeigt.

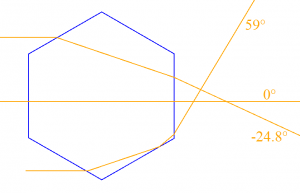
Auch mehrfache totale Reflektionen innerhalb des Kristalls sind möglich. Diese kommen zwar seltener vor können jedoch dazu führen, dass ein Lichtstrahl beinahe in die Ausgangsrichtung zurückgelenkt wird.

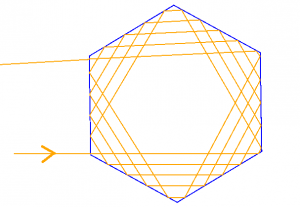
Das Prinzip des Programmes basiert auf dem sogenannten Raytracing. Dies lässt sich grundsätzlich auch auf dem Papier durchführen. Man beginnt einen Strahl zu zeichnen und zeichnet ihn bis er auf eine Grenzfläche auftrifft. Dort wird der Einfallswinkel gemessen und mit dem Brechungsgesetz von Snellius der Ausfallswinkel berechnet. Anschließend setzt man den Strahl entsprechend fort bis er wieder auf eine Grenzfläche trifft oder aber ungehindert das Bild verlässt.

Nach Abschluss des Zählens kann man nun plotten wieviele Strahlen prozentuell in welche Richtung abgelenkt wurden.

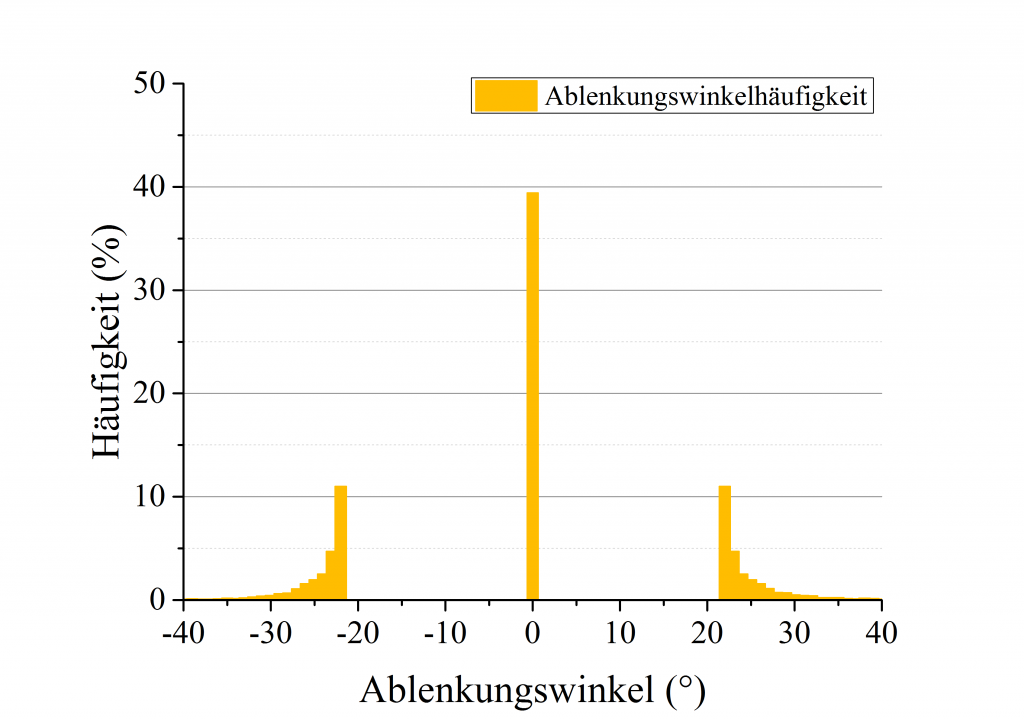
Und auch hier sieht man, dass sofern ein Lichtstrahl abgelenkt wird, diese Ablenkung um mindestens $21^o$ erfolgt. Als zusätzliche Erktenntnis ergibt sich aber auch eine Information über die Lichtintensitätsverteilung der Nebensonne(n). Das Maximum ist klar im Bereich um $22^o$ (also von $21.5^o$ bis $22.5^o$). Danach fällt die Intensität aber stark ab und bei $28^o$ liegt sie bereits unter einem Prozent der Ausgangsintensität.

Somit haben wir die Erklärung für Nebensonnen und Halos gefunden. Im ersteren Fall schweben in der Atmosphäre kleine sechseckige Eiskristallplättchen deren Grundfläche parallel zum Boden orientiert ist. Das Licht wird (abhängig von dessen Wellenlänge) von ihnen auf charakteristische Weise abgelenkt – und zwar für gelb-oranges Licht mindestens in einem Winkel von $21.8^o$.

Lesenwertes und Quellen

Lichterscheinungen und Halos um die Sonne

Brechungsindizes für Eis