Teil 2 – Temperaturbestimmung
Heute geht es darum, wie eine Infrarotkamera es anstellt die Temperatur zu bestimmen. Aber zuvor ein kurzer Rückblick zur Erinnerung.
Was zuletzt geschah
Inhalt der Artikelserie
Teil 1 – Grundlegendes
Teil 2 – Temperaturbestimmung
Teil 3 – Emissionskoeffizient
Teil 4 – Die Messgleichung
Im letzten Eintrag haben wir uns erstmal ganz grundlegend damit beschäftigt wo die Unterschiede zwischen einer Infrarot- und einer Digitalkamera liegen. Die Digitalkamera detektiert hauptsächlich sichtbares reflektiertes Licht aus dem Bereich $400-700\text{nm}$ während die Wärmebildkamera im Infrarot zwischen $1-12 \mu \text{m}$ Licht aufzeichnet. Ein Nanometer ist dabei ein tausendstel von einem Mikrometer. Und ein Mikrometer ein tausendstel eines Millimeters.
Dann haben wir noch einen Blick auf das Planck’sche Strahlungsgesetz geworfen und anhand dessen festgestellt, warum gerade der Bereich $1-12 \mu \text{m}$ für uns interessant ist. Dort liegt bei „üblichen“ Temperaturen nämlich das Maximum der Strahlungsabgabe.
Das Adjektiv „übliche“ steht deswegen unter Anführungszeichen, weil IR-Kameras tatsächlich ja auch in anderen Bereichen zum Einsatz kommen. In der Astronomie zum Beispiel an Bord von Weltraumteleskopen (Herschel Space Observatory, Spitzer Space Telescope, IRAS). Diese detektieren Strahlung im fernen Infrarot. So können zum unter anderem Staubwolken in unserer und in Nachbargalaxien beobachtet werden welche eine Temperatur von nur -130°C haben. Bei diesen Temperaturen wird die meiste Strahlung erst bei einer Wellenlänge von $20 \mu \text{m}$ abgegeben!
Man kann auch in die andere Richtung gehen – was passiert zum Beispiel bei höheren Temperaturen wie – sagen wir mal nicht ganz zufällig – 5500K?
In dieser Abbildung ist das Ergebnis des Planckschen Strahlungsgesetzes für einen 5500K heißen Körper geplottet – dieser hat sein Strahlungsmaximum im gelb-grünlichen Bereich des sichtbaren Spektrums. Diese 5500K sind ca. die Oberflächentemperatur unserer Sonne, und das gezeigte Farbspektrum also jenes, das unsere Augen wahrnehmen können. Bei so hohen Temperaturen bewegen wir uns wieder in dem Bereich, wo Digitalkameras zum fotografieren verwendet werden. Ist ein Körper heiß genug, strahlt er auch im sichtbaren Teil des Spektrums ab! Dies kann man zum Beispiel auch bei Metallen die weit genug erwärmt werden beobachten (Wolframdraht Glühbirne).
Aber in dieser Artikelserie bleiben wir auf der Erde und damit auch bei „alltäglicheren“ Temperaturen.
Temperaturen mit einer Infrarotkamera bestimmen – Das Prinzip
Also, wie kommt man jetzt auf eine Temperatur? Hierfür ist weiterhin das Planck’sche Strahlungsgesetz hilfreich.
\[w(\lambda,T) = \frac{2hc^2}{\lambda^5}\left(\exp{\left(\frac{hc}{\lambda k_B T}\right)}-1\right)^{-1} \]
[expand title=“Ausklappen für Variablenerklärung!“]
Hier steht $c$ für die Lichtgeschwindigkeit, $h$ das Planck’sche Wirkungsquantum, $\lambda$ die Wellenlänge, $k_B$ die Boltzmann Konstante und $T$ für die absolute Temperatur des Körpers.
[/expand]
Zur Erinnerung nochmal die Spektren die sich für verschiedene Temperaturen ergeben.
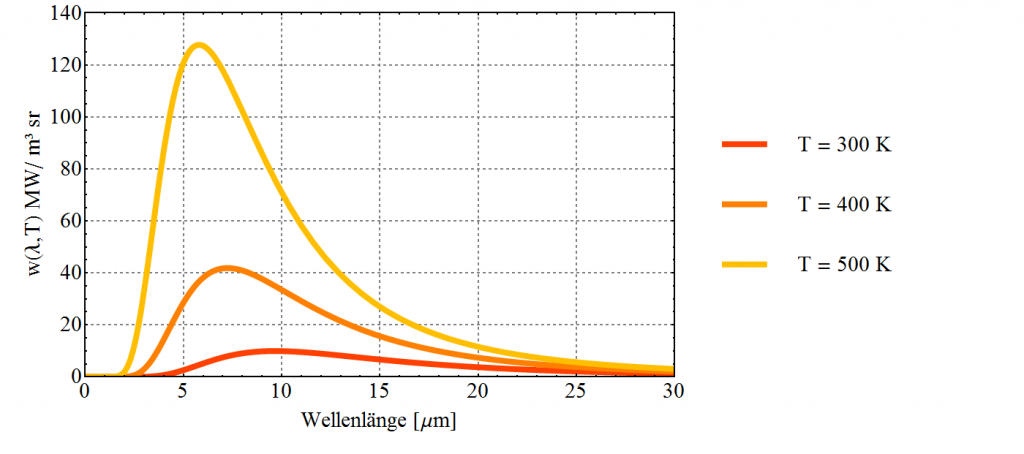
Die Helligkeit die die Kamera sieht
Infrarotkameras die sich dieser häufig verwendeten Methode bedienen haben wenn man so will ein „Problem“ – sie sehen zwar im Infrarotbereich, sind aber farbenblind – wobei Farben als Konzept ohnehin nur im sichtbaren Teil des Spektrums Sinn haben. Dieser Kameratyp kann also nur wahrnehmen, wie hell etwas erscheint wenn eine bestimmte Zeit lang hingesehen wird.
Nun kann man sich wundern – denn es gibt ja aber diese farbenfrohen Thermografie Bilder die man immer sieht, wenns um das Thema geht. Was ist mit denen?
Eigentlich färben diese eben nur die verschiedenen von der Kamera wahrgenommenen Helligkeiten unterschiedlich ein! Jeder Pixel sieht einen anderen Bildausschnitt, und aus jedem trifft eine unterschiedliche Menge an Strahlung auf dem Pixel ein. Anstatt von Grautönen die den Helligkeitswert wiedergeben werden stattdessen Farbwerte zugeordnet.
Jetzt aber zur Temperaturbestimmung. Nehmen wir also an, dass unsere Kamera im Bereich $8-12\mu \text{m}$ etwas sieht – ein typischer Abschnitt. Ziehen wir das Planck’sche Strahungsgesetz heran und sehen uns an, wie das Spektrum für einen 500K (ca. 227°C) heißen Körper aussieht – eine Herdplatte zum Beispiel. Aber diesmal zeichnen wir auch den Bereich ein, in dem die Kamera etwas detektieren kann.
Die Wellenlängen die die IR Kamera wahrnehmen kann liegen innerhalb dieses orangen Bereichs. Aber es ist schon etwas mehr zu sehen. Der Bereich ist nicht einfach nur durch zwei Striche markiert sondern durchweg orange eingefärbt. Dies spielt darauf an, dass die Helligkeit die die Kamera letztlich sieht davon abhängt, wie groß diese orange Fläche ist. Man kann, wenn man die nächste Abbildung betrachtet auch gut sehen, dass diese Fläche für verschieden warme Körper verschieden groß ist. Prinzipiell gilt: Je kühler desto kleiner bzw. je heißer desto größer ist diese.
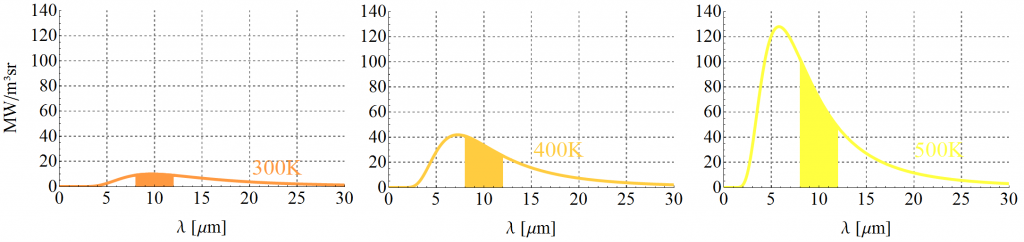
Mathematisch berechnet man – grob gesagt – die Fläche unter einer Kurve mittels Integration. In unserem Fall sieht das zu lösende Integral so aus:
\[ \int_{8 \mu \text{m}}^{12 \mu \text{m}} w(\lambda,T) d \lambda \label{eqn_planck_integral} \]
Wir integrieren also über alle Wellenlängen im Bereich von $8-12\mu \text{m}$. Nun haben wir die Möglichkeit die Größe der Fläche gegen die Temperatur aufzutragen. In der nächsten Abbildung kann man sich das ansehen – und man sieht schon – diese wird mit steigender Temperatur immer größer.
Aus diesem Graph geht auch hervor, weshalb sich die Temperatur gut bestimmen lässt. Die Werte in der Kurve sind alle eindeutig, zu jeder Temperatur gehört genau eine abgestrahlte Leistung pro Fläche und Raumwinkel. Die Kamera misst also eine bestimmte Intensität pro Raumwinkel und muss nurmehr in einer gespeicherten Tabelle nachschlagen, welcher Temperatur diese entspricht.
So weit so gut. Das grundlegende Prinzip hinter der Temperaturbestimmung haben wir nun gelüftet. Im nächsten Artikel betrachten wir das ganze etwas detaillierter – Komplikationen die sich ergeben weil nicht alles ideal ist.
4 Kommentare